Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 29

A aceleração devida á gravidade, a uma altitude y acima da superfície da Terra, pode ser expressa como a = - 9,81 1 + y 6,37   x   10 6   2   onde a   e   y são expressos em m / s 2 e metros, respectivamente. Usado essa expressão, calcule a altura atingida por um projétil disparado verticalmente para o alto, a partir da superfície terrestre, se sua velocidade inicial for de (a) v = 540   m ² s , (b) v = 900   m / s e (c) v = 12,000   m / s .

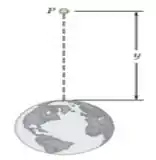
Passo 1

Vamos a mais uma questão de resmat, partiu?

Temos:

v d v d y = a = - 9,81 1 + 4 6,37   x   10 6   2

Quando y = 0 ,   v = v 0 y = y m a x ,   v = 0

Então: ∫ v 0 0 v d v = ∫ 0 y m a x - 9,81 1 + y 6,37   x   10 6   ² d y

Ou - 1 2 v 0 2 = - 9,81   x   - 6,37   x   10 6   1 1 + 4 6,37   x   10 6     0 y m a x

Ou v 0 2 = 62,489   x   10 6 1 - 1 1 + y m a x 6,37   x   10 6  

Ou y m a x = v 0 2 64,4 - v 0 2 6,37   x   10 6

Passo 2

Substituindo os valores temos...

  1. v 0 = 540   m / s : y m a x = ( 540 ) ² 64,4 - ( 540 ) ² 6,37   x   10 6   = 4,53 x   10 3 m  
  2. v 0 = 900   m / s : : y m a x = ( 900 ) ² 64,4 - ( 900 ) ² 6,37   x   10 6   = 12,60   x   10 3 m
  3. v 0 = 12000   m / s : y m a x = ( 12 00 ) ² 64,4 - ( 12 00 ) ² 6,37   x   10 6 ,   = 22,44   x   10 3 m  

Ou

A velocidade 12000   m / s : é aproximadamente a velocidade de escape v R   da Terra. Para v R .

Resposta

  1. y m a x = 4,5 3   x   10 3 m
  2. y m a x = 12,60   x   10 3 m
  3. y m a x = 22,44 x   10 3 m  

y m a x → ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um dado instante de uma corrida de aeronaves, o avião A está voando horizontalmente em linha reta e sua velocidade escalar aumentada a uma taxa de 8 m/s2 . O avião B está voando na mesma altitude q
Uma bola de basquete é solta no chão no ponto A e quica com velocidade vA de intensidade 2,25 m/s como mostrado na figura. Determine o raio de curvatura da trajetória descrita pela bola (a) no ponto A
Os carros de corrida A e B se deslocam em trechos circulares de um autódromo. No instante mostrado na figura, a velocidade de A está decrescendo a uma taxa de 7 m/s² e a velocidade de B está aumentand
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0 que forma um ângulo α com a horizontal. Expresse o raio de curvatura da trajetória do projétil no ponto C em termos de x, v0,
O carvão é descarregado da carroceria de um caminhão basculante com uma velocidade inicial de vA = 2 m/s ∡ 50°. Determine o raio de curvatura da trajetória descrita pelo carvão (a) no ponto A, (b) no