Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 140
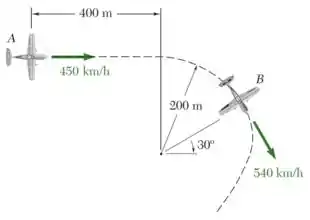
Em um dado instante de uma corrida de aeronaves, o avião A está voando horizontalmente em linha reta e sua velocidade escalar aumentada a uma taxa de 8 m/s2 . O avião B está voando na mesma altitude que o avião A e, à medida que ele contorna um marco, segue uma trajetória circular de 300 m de raio. Sabendo que em um dado instante a velocidade de B começa a decrescer para uma taxa de 3 m/s2 , determine, para as posições mostradas na figura, (a) a velocidade de B em relação a A, (b) a aceleração de B em relação a A.
Passo 1
Primeiro note
(a)Nós temos
A representação grafica dessa equação esta demonstrada abaixo
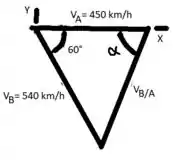
nós temos
ou
e
ou
Passo 2
(b)Primeiro note
Agora
ou
Então
Finalmente
ou
ou
Resposta
Exercícios de Livros Relacionados
Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 12 - 3 t 2m / s , onde t é dado em segundos. Quando t = 1s , a partícula está localizada 10m à esquerda da origem. Determine a a
Uma partícula move-se ao longo de uma trajetória em linha reta de tal maneira que em 4 s ela se move de uma posição inicial s a = - 8m para uma posição s b = + 3m . Então, em mais 5 s, ela move-se de
Uma partícula move-se ao longo de uma linha reta de tal maneira que em 2s ela se move de uma posição inicial s a = + 0,5m para uma posição s b = - 1,5m . Então, em mais 4s , ela move-se de s b para s
Testes revelam que um motorista normal leva em torno de 0,75 s antes de poder reagir a uma situação para evitar uma colisão. Um motorista com 0,1% de álcool no seu sistema leva em torno de 3 s para fa
Conforme um trem acelera uniformemente, ele passa por sucessivas marcas de um quilômetro enquanto se move a velocidades de 2 m/s e, em seguida, 10 m/s. Determine a velocidade do trem quando ele passar