Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 145
Uma bola de basquete é solta no chão no ponto A e quica com velocidade vA de intensidade 2,25 m/s como mostrado na figura. Determine o raio de curvatura da trajetória descrita pela bola (a) no ponto A, (b) no ponto mais alto da trajetória.
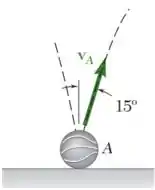
Passo 1
(a)Nós temos
ou
ou
Passo 2
(b)Nós temos
Onde o Ponto B é o ponto mais alto da tragetória, dito isso
Então
ou
Resposta
Exercícios de Livros Relacionados
Um carro parte do repouso e move-se com uma aceleração constante de 1,5 m/s2 até alcançar uma velocidade de 25 m/s. Em seguida, move-se com uma velocidade constante por 60 segundos. Determine a veloci
Uma partícula parte do repouso e move-se ao longo de uma linha reta com uma aceleração a = 30 - 0,2 vm / s 2 , onde v é dado em m/s. Determine o tempo quando a velocidade da partícula for v = 30m / s
Uma esfera é atirada para baixo em um meio com uma velocidade inicial de 27 m/s. Se ela experimenta uma desaceleração de a = - 6 tm / s 2 , onde t é dado em segundos, determine a distância percorrida
Uma partícula está se movendo ao longo de uma linha reta de maneira que sua velocidade é definida como v = - 4 s 2m / s , onde s é dado em metros. Se s=2 m quando t=0, determine a velocidade e a acele
Uma partícula está se movendo ao longo de uma linha reta de tal maneira que a sua aceleração é definida como a = - 2 vm / s 2 , onde v é dado em metros por segundo. Se v = 20m / s quando s=0 e t=0, de