Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 150
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0 que forma um ângulo com a horizontal. Expresse o raio de curvatura da trajetória do projétil no ponto C em termos de x, v0, e g.
E ai gurizada tudo bem? O enunciado pede que a gente determine o raio de curvatura da trajetória do projétil no ponto C em termos de x, v0, e g.
Passo 1
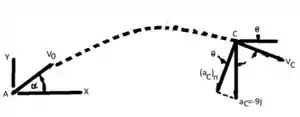
Nós temos
Passo 2
Notando que o movimento horizontal é uniforme, nós temos
Onde
Então
(1)
ou
de modo
Passo 3
Para o movimento vertical uniformemente acelerado nós temos
De cima
Então
(2)
Agora
Substituindo para [Eq. (1)] e [Eq. (2)]
ou
Finalmente, substituindo na expressão para , obtemos
Resposta
Exercícios de Livros Relacionados
A posição de um ciclista viajando ao longo de uma estrada reta é descrita pelo gráfico. Construa os gráficos v - t e a - t .
Um carro esportivo move-se ao longo de uma estrada reta com uma aceleração-desaceleração descrita pelo gráfico. Se o carro parte do repouso, determine a distância s’ que o carro se desloca até parar.
A posição de um ciclista viajando ao longo de uma estrada reta é descrita pelo gráfico. Construa os gráficos v - t e a - t .
Um motociclista partindo do repouso move-se ao longo de uma estrada reta e por 10 s tem uma aceleração, como mostrado. Trace o gráfico v-t que descreve o movimento e descubra distância percorrida em 1
O gráfico v-t de um carro enquanto se move ao longo de uma estrada é mostrado. Trace os gráficos s-t e a-t para o movimento.