Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 11

A aceleração de uma partícula é diretamente proporcional ao tempo t . Quando t = 0 , a velocidade da partícula é v = 16 m / s . Sabendo que v = 15 m / s   e   x = 20 m quando t = 1 s , determine a velocidade, a posição e a distância total percorrida quando t = 7 s .

Passo 1

Temos: a = k t         k = c o n s t a n t e

Agora: d v d t = a = k t

Em: t = 0 ,   v = 16   m / s : ∫ 16 v d v = ∫ 0 t k t   d t

Ou v - 16 = 1 2 k t ²

Ou v = 16 + 1 2 k t ² ( m / s )

Passo 2

Em: t = 1 ,   v = 15   m / s : 15   m . / s = 16   m / s + 1 2 k   x   ( 1 s ) ²

Ou k = - 2   i n . / s 3     e       v = 16 - t ²

Além disso d x d t = v = 16 - t ²

Em: t = 1 s ,   x = 20 i n . : ∫ 20 x d x = ∫ 1 t 16 - t 2 d t

Ou x - 20 = [ 16 t - 1 3 t 3 ] 1 t    

Ou x = 1 3 t ³ + 16 t + 13 3 ( i n . )

Passo 3

Então:

Em: t = 7 s : v 7 = 16 - 7 2 x 7 = - 1 3   x   7 3 + 16   x   7 + 13 3

Quando v = 0 : 16 - t ² = 0   o u   t = 4 s

Em: t = 0 :   x 0 = 13 3

t = 4 s : x 4 = - 1   3 x   4 3 + 16   x   4 + 13 3 = 47   m .

Agora observe que: 0 ≤ t < 4 s :           v > 0 4 s < t ≤ 7 s :           v < 0

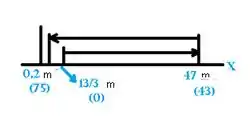
Então: x 4 - x 0 = 47 - 13 3 = 42,67   i n . x 7 - x 4 = 2 - 47 = 45   i n .

Distância total permitida = 42,67 + 45 =   8 7,7   m .

Resposta

v 7 = - 33,0   m / s

x 7 = 2,00   m .

Distância total permitida = 42,67 + 45   m . = 87,7   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que o raio da Terra e 6.370 km, determine o tempo que o telescópio espacial Hubble leva para percorrer uma orbita, considerando que o telescópio percorre uma orbita circular 590 km acima da su
Um satélite vai percorrer indefinidamente uma orbita circular em torno de um planeta se o componente normal da aceleração do satélite for igual a g(R/r)2, onde g e a aceleração da gravidade na superfí
Um satélite percorre uma orbita circular em torno de Marte a uma altitude de 300 km. Após a altitude do satélite ter sido ajustada, constatou-se que o tempo gasto para percorrer uma orbita aumentou em
Determine o raio de curvatura da trajetória descrita pela partícula do Problema 11.96 quando t = 0, A = 3 e B = 1.
A trajetória de uma partícula P e um caracol de Pascal. O movimento da partícula e definido pelas relações r = b(2 + cos θ ) e θ = π t, onde t e θ são expressos em segundos e radianos, respectivamente