Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 108
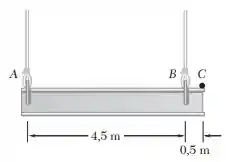
A aceleração do ponto C é de 0,5 m/s² para baixo e a aceleração angular da viga é de 0,8 rad/s² no sentido anti-horário. Sabendo que, no instante considerado, a velocidade angular da viga é nula, determine a aceleração de cada cabo.
Passo 1
Vamos lá resolver mais essa. A velocidade angular da viga é nula, e podemos inferir que a aceleração centrípeta também é nula. Com isso, temos que
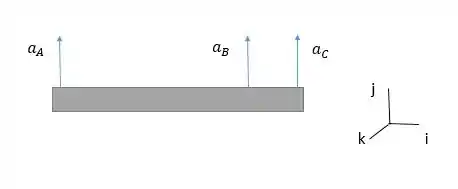
Passo 2
A aceleração do cabo B é:
Resposta
4,5 m/s²; 0,9 m/s²
Exercícios de Livros Relacionados
Um brinquedo em um parque de diversões consiste de um braço em rotação A B tendo uma velocidade angular constante ω A B = 2r a d / s em torno do ponto A e um carrinho montado na extremidade do braço q
O mecanismo de “retorno rápido” consiste de uma manivela A B , o bloco deslizante B e o membro com ranhura C D . Se a manivela tem o movimento angular mostrado, determine o movimento angular do membro
O mecanismo de retorno rápido consiste da manivela C D e do braço com ranhura A B . Se a manivela gira com a velocidade angular e a aceleração angular no instante mostrado, determine a velocidade angu
Um brinquedo em um parque de diversões consiste de um braço em rotação A B que tem uma aceleração angular α A B = 1r a d / s 2 quando ω A B = 2r a d / s no instante mostrado. Também nesse instante o c
As extremidades da barra AB estão confinadas a se deslocarem ao longo das trajetórias mostradas. Em um dado instante, A tem uma velocidade de 2,4 m/s e uma aceleração de 0,9 m/s². Determine a velocida