Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 156
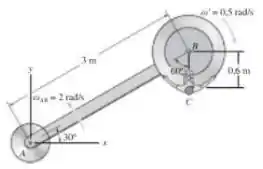
Um brinquedo em um parque de diversões consiste de um braço em rotação tendo uma velocidade angular constante em torno do ponto e um carrinho montado na extremidade do braço que tem uma velocidade angular constante , medida em relação ao braço. No instante mostrado, determine a velocidade e a aceleração do passageiro em .
Passo 1
O exercício em questão envolve uma situação com um sistema em rotação e, logo, o movimento de um ponto em relação ao outro utilizando um sistema de eixos em rotação deve ser analisado. Como o ponto de interesse é o ponto , e ele não possui todas as informações suficientes para cálculo, o que pode ser feito é a determinação das variáveis de posição, velocidade e aceleração do ponto em relação a e, por fim, fazer o mesmo processo para o ponto em relação ao ponto .
Então, a velocidade de em relação a será dada por:
E a aceleração de em relação a é:
Onde:
velocidade angular do sistema de eixos localizado no ponto de interesse em relação ao sistema de referência de origem;
aceleração angular do sistema de eixos localizado no ponto de interesse em relação ao sistema de referência de origem.
Passo 2
Fazendo o diagrama de corpo livre (DCL) será obtido:
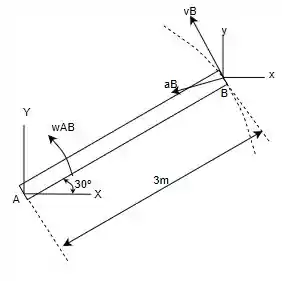
Tal que a velocidade em é:
E a aceleração é:
Em que os sufixos e indicam a aceleração tangente e a normal, respectivamente.
é o vetor posição de até que será:
Considerando o ponto como o centro instantâneo de velocidade nula, a sua velocidade e aceleração serão ambas nulas. Além disso, como o enunciado não fornece a aceleração angular do braço ela será considerada nula. Portanto, teremos:
E:
Além disso, outro parâmetro que pode ser definido é a velocidade angular do referencial em relação ao referencial , tal que será dado pela soma das velocidades angulares envolvidas no problema:
Passo 3
Sendo assim, tendo essas variáveis determinadas juntamente com os valores previamente fornecidos pelo exercício, se torna possível fazer o cálculo dos valores desejados no ponto . Portanto, a velocidade em será dad por:
O vetor representa o vetor distância de até , ou seja:
E, como o passageiro em se encontra no mesmo brinquedo que possui o ponto , eles se movem em conjunto com a mesma velocidade. Então, por isso a velocidade relativa entre esses dois pontos é nula, assim como a aceleração relativa.
Logo:
E:
Como dito antes, o enunciado não fornece valor de aceleração angular e, por isso . Dessa forma, será obtido: