Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 78
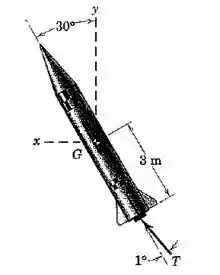
Acima da atmosfera da Terra a uma altitude de onde a aceleração devida à gravidade é de , um determinando foguete possui uma massa total restante de e está direcinado a da direção vertical. Se o empuxo do motor do foguete é de e se o bocal do foguete está inclinado em um ângulo de como mostrado, calcule a aceleração angular do foguete e as componentes e da aceleração do seu centro de massa . O foguete possui um raio de giração centroidal de .
Passo 1
Para calcular a aceleração angular do foguete vamos precisar do seu momento de inércia em relação ao ponto .
Onde é o raio de giração que foi dado no enunciado:
E o momento realizado pela força , em relação a um eixo perpendicular ao plano da página, e que passa pelo ponto é:
Já que é a componente da força que é perpendicular ao corpo do foguete, e é a distância até o centro de massa.
Agora já podemos calcular a aceleração angular:
Passo 2
Para calcular a aceleração do centro de massa podemos usar a segunda lei de Newton em cada uma das direções:
E podemos calcular a componente da força em cada direção usando o ângulo de (inclinado de do foguete somada à inclinação de do bocal):
E então:
E na direção temos que considerar também o peso do foguete:
Resposta
A aceleração angular é e as componentes da aceleração são e .