Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas fundamentais - Ex. 10

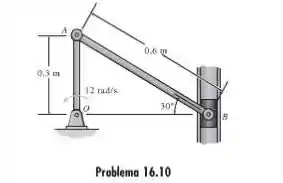
10. Se a manivela AO gira com uma velocidade angular ω = 12   r a d / s , determine a velocidade do pistao B e a velocidade angular da barra AB no instante mostrado.

Passo 1

Nesse tipo de questão, a primeira coisa que temos que fazer é posicionar o eixo que será móvel e aquele que será fixo.

Repare que o pistão em B se move ao longo da barra AB, então vamos posicionar nosso eixo móvel ( x y ) nesta barra.

Feito isso, podemos encontrar a velocidade desse pistão no ponto B pela relação:

v B → = v A → + ω A B → × r → B / A

No entanto, para isso, precisamos encontrar a velocidade do ponto A e a velocidade angular da barra A B ... vamos atrás disso aí!

Passo 2

A velocidade do ponto A , pode ser dada a partir da rotação que a barra A O faz ao redor do eixo fixo O . A relação é:

v A → = ω O A → × r O A →

Considerando os eixos x para a direita, y   para cima e z saindo do plano da página, temos que:

r O A → = 0,3 m   j ^

E pela regra da mão direita, a velocidade angular é:

ω O A → = 12 r a d / s   k ^

Assim, a velocidade será:

v A → = 12 k ^ × 0,3 j ^ = 3,6 k ^ × j ^ = 3,6 - i ^

v A → = -   3,6 m / s   i ^

Agora ficou faltando apenas a velocidade angular da barra A B ... vamos ver se conseguimos encontra-la naquela equação que eu apresentei no Passo 1.

Passo 3

Voltando a nossa primeira equação:

v B → = v A → + ω A B → × r → B / A

Vamos substituir nessa equação o que temos... Além disso, sabemos que a velocidade do pistão B precisa ser na direção do eixo y , certo... logo, podemos escreve-lo como sendo o seu módulo vezes o vetor unitário da direção y

v B → = v B j ^

Além disso, sabemos que a velocidade angular da barra A B precisa estar na direção do eixo z , logo:

ω A B → = ω A B k ^

Substituindo tudo na expressão e a velocidade de A que encontramos:

v B j ^ = - 3,6 i ^ + ω A B k ^ × ( r → B / A )

Precisamos aqui, decompor o vetor posição r → B / A , para isso vamos usar o ângulo de 30º dado e toma cuidado, esse vetor ele vai da posição A até a posição B (cuidado para não fazer o contrário e errar hein!)

r → B / A = 0,6 c o s 30 º i ^ - 0,6 s e n 30 º j ^

r → B / A = 0,519 m i ^ - 0,3 m j ^

Voltando para a nossa expressão:

v B j ^ = - 3,6 i ^ + ω A B k ^ × ( r → B / A )

v B j ^ = - 3,6 i ^ + ω A B k ^ × 0,519 i ^ - 0,3 j ^

v B j ^ = - 3,6 i ^ + 0,519 ω A B   k ^ × i ^ - 0,3 ω A B k ^ × j ^

v B j ^ = - 3,6 i ^ + 0,519 ω A B   j ^ - 0,3 ω A B   - i ^

v B j ^ = - 3,6 i ^ + 0,519 ω A B j ^ + 0,3 ω A B i ^

Guarda essa expressão no coração, por que agora vamos igualar o que está multiplicando i ^ e o que está multiplicando j ^ ...

0 = - 3,6 i ^ + 0,3 ω A B i ^

ω A B = 3,6 0,3 = 12   r a d / s

Opa, encontramos o módulo da nossa velocidade angular da barra A B ... agora é só trabalhar com a parte da equação em j ^ e TEY!, encontramos a velocidade do pistão em B !

v B j ^ = 0,519 ω A B j ^

v B = 0,519 × 12

v B = 6,24 m / s

E para fechar, vamos escrever esses caras vetorialmente:

ω A B → = 12 r a d / s   k ^

v B → = 6,24 m / s   j ^

Resposta

ω A B → = 12 r a d / s   k ^

v B → = 6,24 m / s   j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anel C tem uma raio interno de 55 mm e um raio externo de 60 mm e é posicionado entre duas rodas A e B, cada uma com raio externo de 24 mm. Sabendo que a roda A gira com uma velocidade angular const
A velocidade nominal do tambor B da lixadeira mostrada na figura é de 2.400 rpm. Quando a lixadeira é desligada, observa-se que o tambor, então livre, alcança o repouso em 10 s. Admitindo-se um movime
Uma corda é enrolada em torno de um cilindro de raio r e massa m, conforme mostrado. Sabendo que o cilindro foi solto do repouso, determine a velocidade do centro do cilindro após ele ter se movido pa
Um colar com uma massa de 1 kg é rigidamente preso a uma distância d = 300 mm da extremidade de uma haste fina e uniforme AB. A haste tem uma massa de 3 kg e é de comprimento L = 600 mm. Sabendo que a
O berço de 9 kg é suportado como mostrado por dois discos uniformes que rolam sem deslizar em todas as superfícies de contato. A massa de cada disco é m = 6 kg e o raio de cada disco é r = 80 mm. Sabe