Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 75
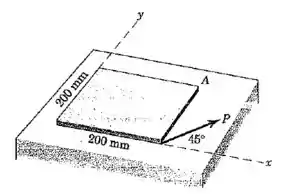
A placa de aço quadrada uniforme tem uma massa de e está em repouso sobre uma superfície horizontal lisa no plano -. Se uma força horizontal é aplicada na direção e sentido mostrado, determine o módulo da aceleração inicial do vértice .
Passo 1
Vamos começar calculando a aceleração do centro de massa da placa. Isso pode ser feito usando apenas a segunda lei de Newton:
Mas além de ter seu centro de massa acelerado (ou seja, além de transladar), a placa também deve ter certa rotação. Vamos procurar a aceleração angular desse movimento de rotação em relação ao centro de massa:
O momento de inércia da placa quadrada em relação ao centro de massa é:
E o momento da força em relação ao centro de massa é:
Onde é metade do comprimento da diagonal do quadrado, já que a força é perpendicular a essa diagonal. Então:
Passo 2
Agora pense o seguinte: quando a placa translada na direção da força (movimento do centro de massa), a acelaração associada a essa translação é a mesma para todos os pontos.
Então o ponto tem uma aceleração na direção da força .
Mas além disso, quando a placa gira em torno do seu centro de massa com aceleração angular , o ponto terá uma outra aceleração associada a esse movimento:
Onde é a posição do ponto em relação ao centro de massa:
E essa aceleração é perpendicular à aceleração do centro de massa.
Passo 3
Agora podemos calcular a aceleração total agindo sobre o ponto :
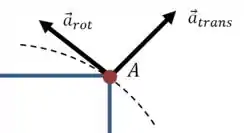
E o módulo dessa soma de vetores pode ser encontrado usando o teorema de pitágoras:
Resposta
A aceleração inicial do vértice é .