Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 79
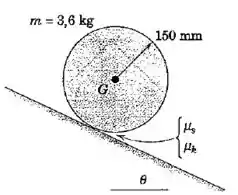
O cilindro maciço homogêneo é liberado a partir do repouso sobre a rampa. Se , e , determine a aceleração do centro de massa e a força de atrito exercida pela rampa sobre o cilindro.
Passo 1
Vamos supor que o cilindro rola sem deslizar. Nesse caso, podemos fazer a seguinte afirmação sobre a relação entre a aceleração do centro de massa e a aceleração angular:
E o diagrama das forças que agem sobre o cilindro fica da seguinte forma:
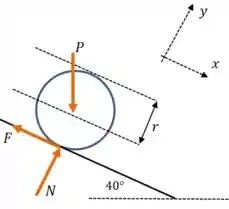
E então podemos aplicar a segunda lei de Newton em cada direção:
E podemos escrever também uma equação para os momentos em relação ao centro do cilindro:
Passo 2
E assim ficamos com um sistema de quatro equações e quatro variáveis desconhecidas:
Vamos substituir os valores numéricos:
E agora resolver para encontrar e . Substituindo a primeira equação na terceira:
E dividindo a segunda equação por dois temos o seguinte:
E pelo resultado anterior:
E substituindo no resultado anterior para encontrar :
Resposta
A aceleração é e a força de atrito é .