Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 98

O bloco A de 10   kg é solto do repouso e desliza para baixo pelo plano liso. Determine a compressão x da mola quando o bloco para instantaneamente.

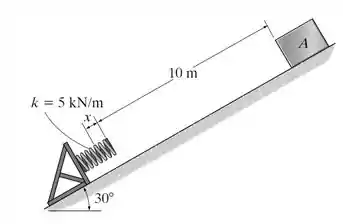
Passo 1

Para equacionar o problema utilizando a conservação da energia, é necessário visualizar o sistema em dois momentos, no instante 1 o bloco é solto para deslizar e no instante 2 o bloco parar instantaneamente após deformar a mola. Conforme a figura abaixo ilustrar.

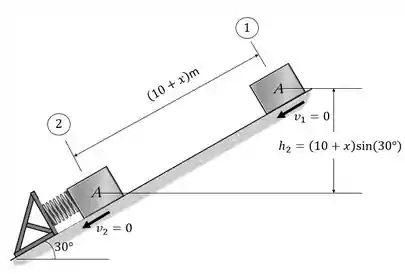
A deformação da mola para quando o bloco parar instantaneamente será a x então a energia potencial elástica é

E k 1 = 1 2 k s 2 2 = 1 2 5000 x 2

Passo 2

Com o sistema analisado agora é possível aplicar a conservação da energia, tendo como referência a posição 1.

E C 1 + E g 1 + E k 1 =   E C 2 + E g 2 + E k 2

1 2 m v 1 2 + g m h 1   + 1 2 k s 1 2   =   1 2 m v 2 2 + g m h 2 +   1 2 k s 2 2

0 + 0 + 0   =   0 + 9,81 10 - 10 + x s i n ⁡ ( 30 ° ) +   2500 x 2

2500 x 2 - 49,05 x - 490,5 = 0

Sendo as duas raizes

x 1 = - 0,4332   m

E

x 2 = 0,4529   m

Somente a raiz positiva admitida como solução.

Resposta

A compressão x da mola quando o bloco para instantaneamente é 453   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um equipamento de massa m está preso em A por duas molas cada uma com rigidez k e comprimento sem deformação b . O equipamento é liberado a partir do repouso neste ponto e cai a uma pequena distância.
O cursor de 0,6k g é liberado a partir do repouso em A e desliza para baixo na guia parabólica lisa (que está localizada em um plano vertical) sob a influência do seu próprio peso e da mola de constan
Calcule a velocidade máxima do cursor B se o sistema é liberado a partir do repouso com x = y . O movimento é no plano vertical. Assuma que o atrito é desprezível. Os cursores possuem massas iguais.
“Bombeando” enquanto balança, o menino aumenta a amplitude de oscilação de θ 0 para θ 1 pela variação abrupta da posição de sentado para a de deitado de costas no início de cada oscilação pra frente e
A corrente de comprimento L é liberada a partir do repouso sobre o plano inclinado liso com x = 0 . Determine a velocidade v dos elos em termos de x .