Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 78
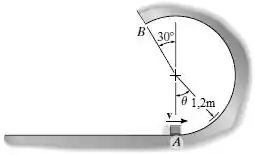
Uma caixa de 2,5 kg é arremessada com uma velocidade de 6 m/s em sobre a pista lisa circular vertical. Determine o ângulo quando a caixa deixa a pista.
Passo 1
O enunciado nos dá as seguintes informações:
Massa da caixa: 2,5 kg;
Velocidade em : m/s;
Pista lisa: força de resistência à tração pode ser desprezada;
Pista circular: trajetória curva;
Raio: m.
Ângulo em :
Nosso objetivo é determinar o ângulo em que a caixa deixa a pista, ou seja, que descola do chão. Como o corpo estará descolado da pista, a força normal será nula .
Primeiramente, desenharemos o Diagrama de Corpo Livre da caixa.
Onde = força peso
= força normal resultante
= aceleração tangencial
=aceleração normal
Lembre-se que a aceleração normal deve apontar no sentido positivo do eixo normal . Como a aceleração tangencial é desconhecida, vamos supor que ela atue na direção de positiva.
Sabemos que m/s2 e que
Passo 2
Agora, utilizaremos as Equações do Movimento. Sabemos que
Aplicando a Equação do Movimento no sentindo do eixo , temos
Aplicando a Equação do Movimento no sentindo do eixo , temos
Passo 3
Sabemos que, pela relação da cinemática,
Logo,
Devemos estabeler uma relação entre e o ângulo para conseguir desenvolver a questão. Utilizando a relação geométrica , onde , temos que
Finalmente temos a relação
Esta é uma EDO homogênea linear de 1o ordem. Utilizaremos as condições iniciais m/s e para resolver a EDO.
Passo 4
Agora iremos igualar o valor de obtido no Passo 2 com o obtido no Passo 3.
Logo,