Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 241
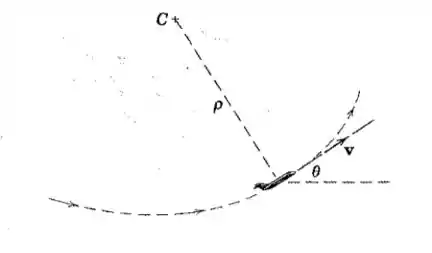
Uma aeronave a jato faz um desvio ascendente em uma curva vertical como apresentado. Quando passa a posição onde , sua velocidade é de e está diminuindo na taxa de por segundo. Se o raio de curvatura da trajetória de voo é de neste ponto, calcule as respectivas componentes horizontal e vertical, e , da aceleração da aeronave.
Passo 1
Vamos começar pensando em coordenadas polares, depois a gente pode projetar tudo nas coordenadas retangulares.
A aceleração tem duas componentes: uma normal (que aponta para o centro da trajetória) e uma tangencial (que é tangente à trajetória).
A normal multa a direção da velocidade, e a tangencial muda o módulo da velocidade:
Ótimo, já temos tudo o que precisamos.
Passo 2
Vamos começar calculando a derivada do módulo da velocidade. O próprio enunciado já diz que ela diminui pela seguinte “taxa”:
Com raras exceções, “taxa” é uma outra palavra para derivada! Ou seja:
Passo 3
E agora para calcular a aceleração normal é só usar a fórmula:
Acabou? Não! Esses são os módulos das acelerações tangencial e normal, mas essas acelerações são vetores nas direções da tangente e do raio, o que a questão pediu foram as acelerações nas coordenadas e .
É só tirar proveito daquele ângulo ali!
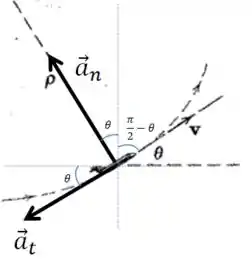
E agora projetando os vetores (não esqueça dos sinais):
Ou seja:
Resolvido!
Resposta
As componentes das acelerações são e .