Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 25
Se o motor enrola o cabo com uma aceleração de 3 m/s², determine as reações nos apoios A e B. A viga tem massa uniforme de 30 kg/m, e a caixa tem massa de 200 kg. Despreze a massa do motor e das polias.
Passo 1
Da geometria do problema, sabemos que:
Em que é o deslocamento da caixa, é o deslocamento do cabo e l é o comprimento total do cabo. E consequentemente, temos:
Para a resolução do exercício, iremos analisar o diagrama a seguir:
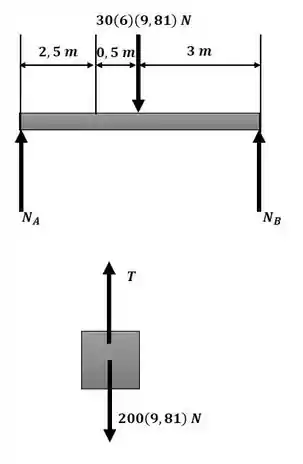
Com isso, podemos aplicar o somatório de forças na direção y para a caixa:
Passo 2
Como temos dois cabos ligados na viga, , logo, aplicando o somatório de momento em relação ao ponto A, temos:
Passo 3
Agora iremos aplicar o somatório de forças na direção y para a viga:
Resposta
Exercícios de Livros Relacionados
4/105) A corrente de elos de comprimento total L e de massa ρ por unidade de comprimento é liberada a partir do repouso em x = 0 no mesmo instante em que a plataforma parte do repouso em y = 0 e se de
4/109) Uma corda ou uma corrente com elos articulados do tipo usado em bicicleta decomprimento L e massa ρ por unidade de comprimento é liberada a partir do repouso com x = 0 . Determine a expressão p
4/112) A corrente de massa ρ por unidade de comprimento passa sobre a pequena polia que gira livremente e é liberada a partir do repouso com apenas um pequeno desequilíbrio h para iniciar o movimento
4/111) Substitua a corrente empilhada no Prob.4/92 por um rolo de corda de massa ρ por unidade de comprimento e comprimento total L como mostrado e determine a velocidade da seção em queda em termos d
A bola de 250g é suportada pelo jato vertical de água doce que escoa a partir do bocal com 12m m de diâmetro a uma velocidade de 10m / s . Calcule a altura h da bola acima do bocal. Suponha que o esco