Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 19
O vagão em de 800 kg está ligado ao vagão em de 350 kg por um engate de mola. Determine a extensão da mola se (a) as rodas de ambos os vagões estão livres para rodar e (b) os freios são aplicados a todas as quatros rodas do vagão , fazendo com que as rodas escorreguem. Suponha .
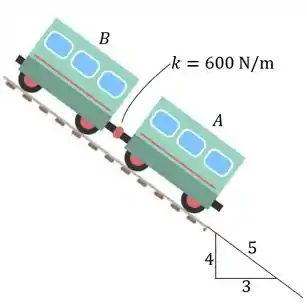
Passo 1
O enunciado nos dá os seguintes dados:
Massa do vagão : kg;
Massa do vagão : kg;
Coeficiente de atrito cinético do vagão : .
Na letra (a) devemos determinar a extensão da mola se as rodas de ambos os vagões estão livres para rodar, ou seja, a força de atrito será nula pois não exerce nenhuma ação para impedir que as rodas rodem.
Na letra (b) devemos determinar a extensão da mola quando os freios são aplicados a todas as quatros rodas do vagão , fazendo com que as rodas escorreguem. Neste caso, devemos considerar a força de atrito no vagão
Passo 2
Primeiramente, vamos resolver a letra (a).
Como não nos foi dito nada sobre a velocidade ou aceleração, vamos considerar que o sistema vagão -vagão tenha uma aceleração não nula .
Para descobrir esta aceleração, vamos desenhar o diagrama de corpo livre do sistema e em seguida vamos aplicar a Equação de Movimento.
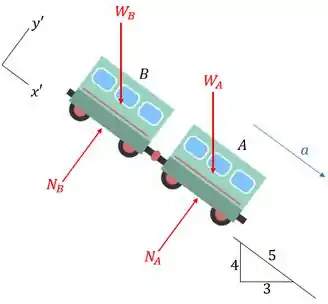
No eixo ’:
Esta é a aceleração em ambos os vagões, uma vez que eles andam juntos.
Para descobrir a extensão da mola, vamos avaliar o diagrama de corpo livre de um dos vagões. Vamos escolher o vagão . Em seguida, vamos aplicar a Equação do Movimento.
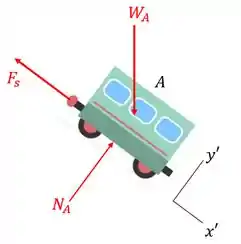
A força é a força elástica exercida pela mola.
No eixo ’:
Logo, temos que
Passo 3
Agora vamos resolver a letra (b).
Neste caso, como o vagão irá freiar, sabemos que o sistema vagão -vagão terá uma aceleração não nula .
Para descobrir esta aceleração, vamos avaliar o diagrama de corpo livre do sistema, uma vez que os vagões andam juntos.
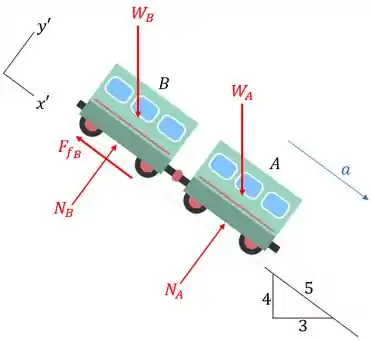
Sabemos que, por definição, a força de atrito é dada por , logo, para o vagão , temos que
Aplicando a Equação de Movimento no eixo para o vagão desenhado no diagrama de corpo livre abaixo, obtemos
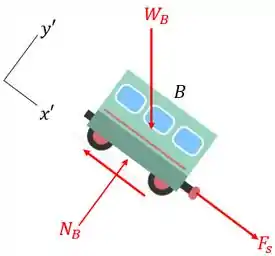
Agora que sabemos o valor de , temos que
Vamos voltar para a análise do sistema. Aplicando a Equação do Movimento no eixo ’, obtemos:
Esta é a aceleração em ambos os vagões.
Para descobrir a extensão da mola, vamos avaliar novamente o diagrama de corpo livre do vagão , aplicando a Equação do Movimento.
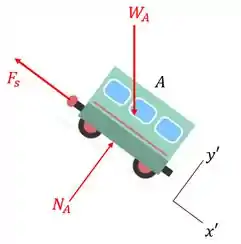
A força é a força elástica exercida pela mola.
No eixo ’:
Logo, temos que