Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 155

A água deixa o impulsor da bomba centrífuga com uma velocidade de 25 m/s e aceleração de 30 m/s², ambas medidas em relação ao impulsor ao longo da linha da pá AB. Determine a velocidade e a aceleração de uma partícula de água em A na medida em que ela deixa o impulsor no instante mostrado. O impulsor gira com uma velocidade angular constante de ω = 15   r a d / s .

Passo 1

Começaremos o exercício esquematizando o eixo de referência para rotação xyz, que estará sob o impulsor conforme o diagrama a seguir:

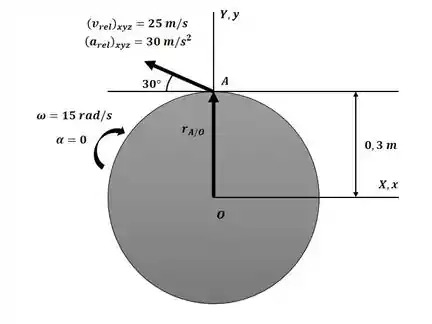
Sendo assim, o movimento com relação ao eixo de referência é descrito por:

v → O = a → O = 0

ω = - 15 k →   r a d / s

ω ˙ = 0

Da figura ainda temos:

r → A / O = 0,3 j →   m

v → r e l x y z = - 25 c o s 30 ° i → + 25 s e n 30 ° j → = - 21,65 i → + 12,5 j →   m / s

a → r e l x y z = - 30 c o s 30 ° i → + 30 s e n 30 ° j → = - 25,98 i → + 15 j →   m / s 2

Passo 2

Agora iremos aplicar a equação da velocidade relativa para os pontos A e O:

v → A = v → O + ω × r → A / O + v → r e l x y z

v → A = 0 + - 15 k → × 0,3 j → + - 21,65 i → + 12,5 j →

v → A = - 17,2 i → + 12,5 j →   m / s

Passo 3

Agora iremos aplicar a equação da aceleração relativa para os pontos A e O com base no diagrama do passo 1:

a → A = a → O + ω ˙ A O × r → A / O + ω A O × ω A O × r → A / O + 2 ω A O × v r e l x y z + a r e l x y z

a → A = 0 + - 15 k → × - 15 k → × 0,3 j → + 2 - 15 k → × - 21,65 i → + 12,5 j → + ( - 25,98 i → + 15 j → )

a → A = [ 349 i → + 597 j → )

Resposta

v → A = - 17,2 i → + 12,5 j →   m / s

a → A = [ 349 i → + 597 j → )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As duas hélices com 800 mm de raio giram no sentido anti-horário com uma velocidade angular constante ω = θ ˙ = 2r a d / s em torno do eixo em O montado em um bloco deslizante. A aceleração do bloco é
Com referencia às hélices e o bloco deslizante do mancal do Prob. 5/123 onde a O = 3 m / s 2 . Se θ ¨ = 5 r a d / s 2 e θ ˙ = 0 quandoθ = 0 , encontre a aceleração do ponto A para esse instante.
Um recipiente para resíduos é descarregado pelo mecanismo ativado hidraulicamente. Se a haste do pistão parte do repouso na posição indicada e possui uma aceleração de 0,5 m/s² no sentido mostrado, ca
15.221. A barra dobrada mostrada na figura gira à taxa constante 1 3 rad /s. Sabendo que o colar C se desloca na direção do ponto D com uma velocidade relativa constante u 1 m/s, determine, para a pos
16.109. O disco está se deslocando para a esquerda de tal maneira que ele tem uma aceleração angular α = 8 r a d / s 2 e velocidade angular ω = 3 r a d / s no instante mostrado. Se ele não desliza em