Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 74
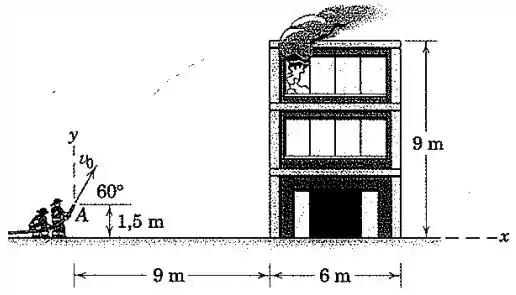
Água escoa do bocal em , que está acima do solo. Determine as coordenadas do ponto de impacto do fluxo se a velocidade inicial da água é
(a) e
(b) .
Passo 1
(a) Pessoal, a primeira coisa que a gente tem que verificar é se a água se impacta com a lateral esquerda do prédio, ou seja, temos que analisar o que acontece quando .
Para o movimento horizontal, temos:
Ou seja, quando , temos .
Passo 2
Agora, vejamos a que altura o fluxo de água está quando . Pra isso, vamos usar a fórmula para aceleração constante:
Usando o tempo , temos:
Então, como a altura do prédio é justamente , o ponto de impacto deve ser na quina da parede lateral com o topo, no ponto de coordenadas .
Passo 3
(b) Analogamente, fazemos esse teste para , pra saber se a água colide com a parede lateral:
Desse modo, como , a água não se choca com a parede lateral esquerda, passando por cima do prédio.
Passo 4
Show! Agora, como o topo do prédio está em , vamos calcular em que ponto de temos . Usando a equação obtida no passo anterior, vamos procurar um valor de em que tenhamos , ok?
Essa equação vai nos dar dois valores de possíveis, mas queremos o maior deles porque o fluxo de água estará cruzando o prédio na descida, não na subida, beleza? Então:
Agora, basta aplicar esse valor de na equação do movimento horizontal:
Como , o fluxo de água não toca o topo do prédio, só cai no chão. Então, o ponto de impacto vai ser .
Resposta
(a)
(b)