Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 39

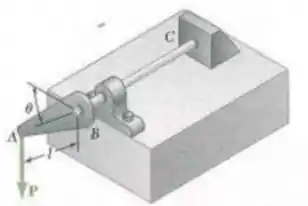
Uma alavanca AB é presa ao eixo horizontal BC que passa atravpes de uma mancal e é soldado a um suporte fixo em C. A constante de mola torcional do eixo BC é K, ou seja, é necessário um binário de intensidade K para girar a extremidade B de 1 radiano. Sabendo que o eixo não está torcido quando AB é horizontal, determine o valor de θ correspondente à posição de equilíbrio quando P = 100 N ,     l = 250 m m   e   K = 12,5   N ⋅ m / r a d .

Passo 1

Primeiro vamos entender o problema! Temos uma força P aplicada na ponta do eixo, ele quer o valor de θ no equilíbrio.

Logo, precisamos encontrar as funções correspondente para derivarmos e usar no trabalho virtual. Assim teremos nossa equação geral.

Passo 2

Achou um pouco complicado? Vamos destrinchar! Assumindo l como a distancia do ponto B ate o ponto A, e y A   como a altura vertical de B até A:

y A = l   s e n   θ

Derivando essa equação:

d y A =   l c o s θ d θ

Passo 3

Pronto! Já temos a relação da força P, então basta utilizarmos o trabalho virtual que encontraremos a resposta. Lembrem-se de sempre checar essas derivadas no meio do processo, derivadas desse tipo as vezes enganam 😊!

Continuando a aplicar o trabalho virtual:

d U =   P d y A - M d θ = 0

P l c o s θ d θ - K θ d θ = 0

Isolando o nosso θ :

θ c o s θ = P l K = 100 N 0.250 m 12.5 N ⋅ m / r a d

θ c o s θ = 2

θ = 59 °

Resposta

θ = 59 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

31- Determine a força N exercida na tora por cada garra do pegador de lenha mostrado.
33- Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C . As con
68- A figura mostra a vista lateral de uma claraboia uniforme de massa m e com centro de massa na metade da distância entre A e O . A clarabóia é contrabalançada pela ação da mola, que tem uma rigidez
73- Os roletes nas extremidades da barra uniforme A B , de 10k g , se movem livremente nas guias horizontal e vertical, como mostrado. Determine a posição de equilíbrio θ para a barra sob a ação de um
71- O painel retangular uniforme de massa m e centro de massa em G é guiado por roletes- o par superior na guia horizontal e o par inferior na guia vertical. Determine a força P , aplicada a extremida