Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 57

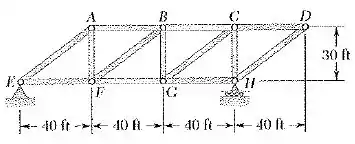
Determine o movimento vertical do nó D se o comprimento do elemento BF é aumentado em 1.5 in.(Dica: aplique uma carga vertical no nó D e, usando os métodos do Capítulo 6, calcule a força exercida pelo elemento BF nos nós B e F. Em seguida, aplique o método do trabalho virtual para um deslocamento virtual que resulta no aumento específico no comprimento do elemento BF. Esse método deve ser usado somente para pequenas mudanças nos comprimentos dos elementos.)

Passo 1

Primeiro vamos lembrar que, a soma dos momentos tem que ser igual a 0 e a soma das forças tem que ser igual a 0. Desse modo, no momento teremos:

∑ M H = 0

Então, note que:

- P 40   f t + E 120   f t = 0

Logo,

E = P 3

De outra maneira temos:

∑ F y = 0

Então, note que:

3 5 F B F - P 3 = 0

Logo,

F B F = 5 9 P

Passo 2

Para o trabalho virtual, vamos primeiro remover o membro BF e substituir por suas forças F B F e - F B F , nos pinos F e B.

Então o trabalho virtual é dado por:

d U = 0

Implica que:

P d D + F B F d r F + - F B F d r B = 0

Portanto:

P d D + F B F ( d r B cos ⁡ θ B - d r F cos ⁡ θ F ) = 0

Observe que

d r B cos ⁡ θ B - d r F cos ⁡ θ F = d B F

Portanto:

P d D - F B F d B F = 0

Substituindo os valores que a questão nos oferece, teremos:

P d D - 5 9 P ( 1.5   i n ) = 0

Logo,

d D =   + 0.833   i n .

Resposta

d D =   + 0.833   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O virabrequim está sujeito a um torque M = 75 N ⋅ m . Determine a força compressiva vertical F aplicada ao pistão para o equilíbrio quando θ = 60 ° .
Determine o peso do bloco G necessário para equilibrar a balança diferencial quando a carga F de 100N( ≈ 10k g ) é colocada na panela. A balança está em equilíbrio quando a carga e o bloco não estão n
Se a carga F pesa 100N e o bloco G pesa 10N , determine sua posição x para o equilíbrio da balança diferencial. A balança está em equilíbrio quando a carga e o bloco não estão na balança.
A placa de ventilação é apoiada em B por um pino. Se ela pesa 75N e tem um centro de gravidade em G , determine a rigidez k da mola de modo que a placa permaneça em equilíbrio em θ = 30 ° . A mola est
Uma força horizontal W de intensidade de 324 N é aplicada ao mecanismo em C. Desprezando o peso do mecanismo, determine o valor de θ correspondente ao equilíbrio. A constante da mola é k = 3.6k N / m