Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 33

Uma força W de intensidade de 600 N é aplicada ao mecanismo articulado em B. A constante da mola é de k = 2.5   k N / m , e a mola está indeformada quando AB e BC são horizontais. Desprezando o peso do mecanismo e sabendo que l = 300   m m , determine o valor de θ correspondente ao equilíbrio.

Passo 1

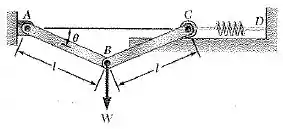
Primeiro vamos entender o problema! Temos uma força W aplicada em B. A mola não é deformada quando AB e BC são horizontais, ele quer o valor de θ no equilíbrio.

Logo, precisamos encontrar as funções correspondente para derivarmos e usar no trabalho virtual.

Passo 2

Achou um pouco complicado? Vamos destrinchar!

Observe na figura o triângulo Δ A B B ' , o ângulo θ é entre a hipotenusa AB e o cateto AB’. Desse modo:

cos ⁡ θ = A B ' A B

Assumindo que, x c = 2 A B ' e que l = A B , temos:

x c = 2 l c o s   θ

Derivando:

d x c = - 2 l s i n   θ   d θ

Também podemos tirar outra relação. Note que:

sin ⁡ θ = B B ' A B

Assumindo, y b = B B ' , temos:

y b = l s i n   θ

Derivando,

d y b = l c o s   θ d θ

Passo 3

Já estamos quase terminando! Vamos lembrar que a força na mola é dada por:

F = k s

Onde s é o alongamento da mola, logo:

s = 2 l - A C = 2 l - x c

Portanto,

F = k ( 2 l - x c )

F = k ( 2 l - 2 l c o s   θ )

F = 2 k l ( 1 - cos ⁡ θ )

Passo 4

Pronto! Já temos a relação da força F, então basta utilizarmos o trabalho virtual que encontraremos a resposta.

Sabemos que, o trabalho virtual é 0. Ou seja,

d U = 0

E como,

d U = F d x c + W d y b

Temos:

F d x c + W d y b = 0

Logo,

2 k l 1 - cos ⁡ θ - 2 l s i n   θ   d θ + W l c o s   θ d θ = 0

Isolando, teremos:

4 k l 2 1 - cos ⁡ θ sin ⁡ θ = W l c o s   θ

1 - cos ⁡ θ tan ⁡ θ = W 4 k l

Portanto,

1 - cos ⁡ θ tan ⁡ θ = 600 4 * 2500 * 0.3

1 - cos ⁡ θ tan ⁡ θ = 0.2

Agora só resolver, e teremos nossa resposta.

θ = 40.22 °  

Resposta

θ = 40.22 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o mecanismo mostrado, a mola é descomprimida quando θ = 0. Determine o ângulo θ para a posição de equilíbrio e especifique a rigidez mínima da mola k que limitará θ a 〖30〗 ^ ∘. A haste DE passa l
A energia potencial de um sistema mecânico é dada porV = 6 x 4 - 3 x 2 + 5 , onde x é a coordenada de posição que define a configuração do sistema de um único grau de liberdade. Determine os valores d
Determine a força Q na mandíbula do cisalhamento para a força 400-N aplicada com θ = 30 ∘. (Dica: substitua a força 400-N por uma força e um par no centro da engrenagem pequena. O deslocamento angular
O pequeno cilindro de massa me raio r está confinado a rolar na superfície circular do raio R. Pelos métodos deste artigo, prove que o cilindro é instável no caso (a) e estável no caso (b).
A barra uniforme de massa m e comprimento L é suportada no plano vertical por duas molas idênticas, cada uma de rigidez k e comprimida a uma distância δ na posição vertical θ = 0. Determine a rigidez