Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 9
Determine o momento resultante produzido pelas forças em relação ao ponto .
Passo 1
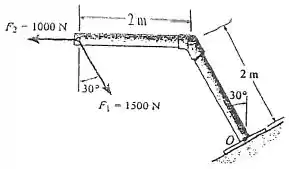
Para determinar o momento resultante das forças, é necessário determinar a distância do ponto até o ponto de atuação de cada força onde os momentos serão aplicados. Assim, os eixos e serão considerados respectivamente na linha horizontal e na linha vertical.
Logo, para os componentes horizontais das forças, a distância até os braços dos momentos serão ambos de:
E para o componente vertical da força será de:
Passo 2
Portanto, assumindo que os momentos positivos ajam no sentido anti-horário, tem-se que:
Resposta
Exercícios de Livros Relacionados
Determine a direção θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza o momento máximo em relação ao ponto A . Calcule esse momento.
As pinças são usadas para prender as extremidades do tubo de perfuração P . Determine o torque (momento) M P que a força apliada F = 750N exerce sobre o tubo em relação ao ponto P como uma função de θ
Sérios danos ao pescoço podem ocorrer quando um jogador de futebol americano é atingido na proteção de rosto de seu capacete da maneira mostrada, causando um mecanismo de guilhotina. Determine o momen
Determine o momento da força F em relação ao ponto A como uma função de θ . Represente os resultados de M (ordenada) em função de θ (abscissa) para ( 0 ° ≤ θ ≤ 180 ° ) .
Determine o ângulo θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza um momento máximo e um momento mínimo em relação ao ponto A . Além disso, quais são as intensidades desses momentos máximo e