Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 85
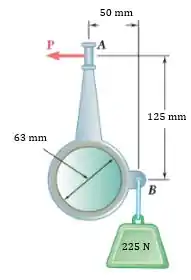
Uma alavanca de peso desprezível é montada com folga em um eixo fixo de de diâmetro. Sabendo que o coeficiente de atrito estático entre o eixo fixo e a alavanca é , determine a força necessária para iniciar a rotação da alavanca no sentido anti-horário.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Observe o diagrama abaixo:
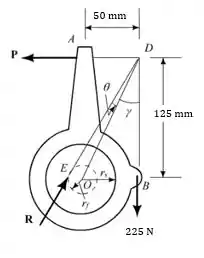
A distância do centro da polia até a linha de ação de é:
O ângulo é dado por:
Passo 2
A distância é dada por:
Logo, o ângulo é dado por:
Portanto:
Passo 3
A força será então:
Resolvendo, teremos:
Resposta
Exercícios de Livros Relacionados
A barra A B é ligada aos colares que podem deslizar sobre as barras inclinadas mostradas na figura. Uma força P é aplicada no ponto D localizado a uma distância a da extremidade A . Sabendo que o coef
O bloco A de 90N e o bloco B de 135N estão apoiados em um plano inclinado que é mantido na posição mostrada na figura. Sabendo que o coeficiente de atrito estático é 0,15 entre todas as superfícies de
Para ser de uso prático, o dispositivo de segurança descrito no problema anterior deve deslizar livremente ao longo do trilho quando puxado para cima. Determine o maior valor admissível do coeficiente
Um trabalhador move vagarosamente um caixote com 50k g para a esquerda ao longo de uma plataforma de carga aplicando uma força P no canto B como mostra a figura. Sabendo que o caixote começa a inclina
Uma barra delgada de comprimento L está apoiada entre um pino C e a parede vertical e sustenta uma carga P na extremidade A . Sabendo que o coeficiente de atrito estático entre o pino e a varra é 0,15