Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 133

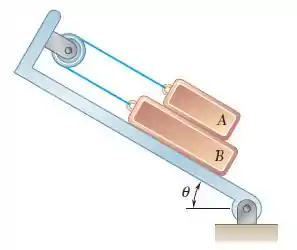
O bloco A de 90   N e o bloco B de 135   N estão apoiados em um plano inclinado que é mantido na posição mostrada na figura. Sabendo que o coeficiente de atrito estático é 0,15 entre todas as superfícies de contato, determine o valor de θ para que o movimento seja iminente.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos analisar o diagrama de corpo livre do bloco A :

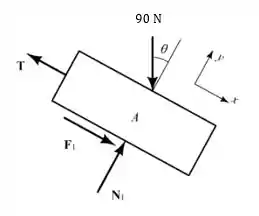
Assumindo a direção dos eixos como mostrado na figura, temos que:

∑ F y = 0

N 1 - 90 cos ⁡ θ = 0

N 1 = 90 cos ⁡ θ

Temos também que:

F 1 = μ s N 1

Logo:

F 1 = 0,15 90 cos ⁡ θ

F 1 = 13,5 cos ⁡ θ

Passo 2

Temos também que:

∑ F x = 0

90 sen ⁡ θ + F 1 - T = 0

Logo:

T = 90 sen ⁡ θ + 13,5 cos ⁡ θ

Passo 3

Vamos analisar o diagrama de corpo livre do bloco B :

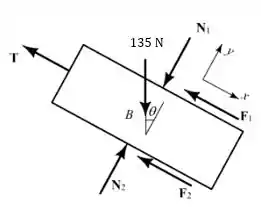
Assumindo a direção dos eixos como mostrado na figura, temos que:

∑ F y = 0

N 2 - 135 cos ⁡ θ - N 1 = 0

N 2 = 225 cos ⁡ θ

Temos também que:

F 2 = μ s N 2

Logo:

F 2 = 0,15 225 cos ⁡ θ

F 2 = 33,75 cos ⁡ θ

Passo 4

Temos também que:

∑ F x = 0

135 sen ⁡ θ - T - F 1 - F 2 = 0

Logo:

T = 135 sen ⁡ θ - 47,25 cos ⁡ θ

Como temos duas equações com valor de T , podemos igualar e equacionar:

90 sen ⁡ θ + 13,5 cos ⁡ θ = 135 sen ⁡ θ - 47,25 cos ⁡ θ

Temos que:

45 sen ⁡ θ = 57,75 cos ⁡ θ

tan ⁡ θ = 57,75 45

Resolvendo, temos que, o ângulo para o qual o movimento é iminente é:

θ = tan - 1 ⁡ 1,28333

θ = 52,074 °

Resposta

θ = 52,074 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força horizontal P que deverá ser aplicada perpendicularmente ao cabo da manivela em A para que uma força compressiva de 12k N atue no material. Cada rosca quadrada tem diâmetro médio de 2
Prove que o avanço l deverá ser menor que 2 π r μ s para que o parafuso mostrado na Figura 8.15 seja “autotravante”.
Uma força P=25N é apenas sufi ciente para impedir que o cilindro de 20k g desça. Determine a força necessária P para iniciar o levantamento do cilindro. A corda passa por um pino áspero com duas volta
O cilindro de 20k g A e o cilindro de 50k g B estão ligados por meio de uma corda que passa emtorno de um pino áspero por duas voltas e meia. Se os cilindros estão na iminência de movimento, determine
O veículo, que tem massa de 3,4M g , deve descer a rampa com velocidade constante, sendo para isso sustentado pela corda enrolada na árvore e mantida esticada pelo homem. Se as rodas estão livres para