Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 19
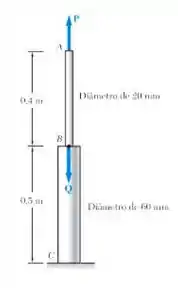
Ambas as partes da barra ABC são feitas de um alumínio para o qual Sabendo que a intensidade de P é 4 kN, determine (a) o valor de Q e modo que o deslocamento em A seja zero e (b) o deslocamento correspondente de B.
Passo 1
E ai gurizada tudo belezinha? Para determinarmos o valor de Q e modo que o deslocamento em A seja zero, vamos começar calculando a área das seções AB e BC,
Agora vamos calcular o alongamento de ambas as seções
Alongamento:
Notem que a força do elemento BC é compressiva então:.
Passo 2
Para deflexão ser zero em A, temos que considerar que:
Resposta
Exercícios de Livros Relacionados
Um eixo de diâmetro 45mm é feito de um aço com 250MPa de resistência ao escoamento na tração. Usando o critério da máxima energia de distorção, determinar a intensidade da força P, para que o início d
Para o estado plano de tensões mostrado, determinar dois valores de σ y para que a máxima tensão de cisalhamento seja de 70M P a .
O estado plano de tensões mostrado ocorre em um componente estrutural feito de aço com σ e = 250M P a . Usando o critério da máxima tensão de cisalhamento, determinar se o escoamento ocorre quando: (a
Um eixo de 36m m de diâmetro é feito de uma classe de aço, com uma resistência ao escoamento na tração de 250M P a . Usando o critério da máxima tensão de cisalhamento, determinar a intensidade do tor
O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, com uma resistência ao escoamento na tração de 240M P a . Determinar o coeficiente de segurança, em relação ao escoam