Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 74

Para o estado plano de tensões mostrado, determinar dois valores de σ y para que a máxima tensão de cisalhamento seja de 70   M P a .

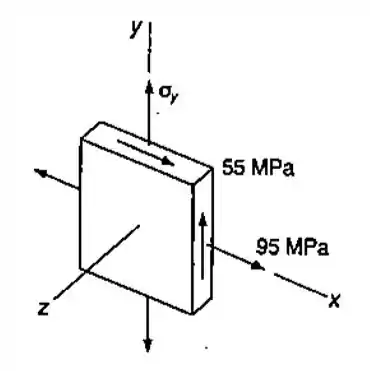
Passo 1

Para resolver essa questão a primeira coisa e a mais importante é saber identificar corretamente as tensões normais e cisalhantes, neste caso será o seguinte:

σ x = 95   M P a

σ z = 0   M P a

τ x y = 55   M P a

Passo 2

Vamos achar a tensão média, que é o centro do ciclo de mohr da seguinte forma:

σ m é d = σ x + σ z 2

σ m é d = 95 + 0 2

σ m é d = 47,5   M P a

Passo 3

Fazendo:

R = σ x - σ z 2 2 + τ x y 2

R = 95 - 0 2 2 + 55 ²

R = 5281,25

R = 72,67   M P a

Passo 4

Agora vamos calcular as tensões normais máxima e mínima:

σ m á x = σ m é d + R

σ m á x = 47,5 + 72,67 = 120,17   M P a

σ m í n = σ m é d - R

σ m í n = 47,5 - 72,67 = 25,17   M P a

Passo 5

Desta forma os dois valores que σ y pode assumir são:

σ y = 120,17   M P a

Ou

σ y = 25,17   M P a

Resposta

σ y = 120,17   M P a

σ y = 25,17   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine as deformações normais médias ao longo do lado AB e das diagonais AC e DB.
A chapa retangular é submetida a deformação mostrada. Determine a deformação por cisalhamento média γ x y da chapa.
A chapa retangular é submetida à deformação mostrada pelas linhas tracejadas. Determine as deformações normais médias ao longo da diagonal AC e do lado AB.
A forma original da peça de borracha é retangular e ela é submetida à deformação mostrada pelas linhas tracejadas. Determine a deformação normal média ao longo da diagonal DB e do lado AD.
A forma original da peça de borracha é retangular. Determine a deformação por cisalhamento média, se os cantos B e D forem submetidos a deslocamentos que provoquem a distorção da borracha mostrada pel