Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 84
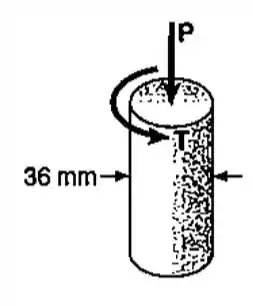
Um eixo de de diâmetro é feito de uma classe de aço, com uma resistência ao escoamento na tração de . Usando o critério da máxima tensão de cisalhamento, determinar a intensidade do torque , para que o início do escoamento ocorra quando .
Passo 1
Todos nós sabemos que existe um limite de carga para que as estruturas mecânicas não caiam em nossas cabeças. Esse limite é dado pela tensão aplicada a uma certo ponto da estrutura e pode ser definido segundo diversos critérios. Neste problema vamos utilizar o da máxima tensão de cisalhamento.
O critério da máxima tensão de cisalhamento é dado da seguinte forma:
Ok, mas e o torque aonde isso vai aparecer?
Ótima pergunta jovem, ao final vamos aplicar a equação do torque em relação à tensão de cisalhamento:
Passo 2
Neste exercício as tensões não foram fornecidas logo de cara então vamos ter de calculá-las a partir da área e da força aplicada:
Negativo porque é uma compressão e o raio é igual à metade do diâmetro:
E
Já que não há forças em .
Passo 3
Agora vamos calcular a máxima tensão cisalhante segudo o nosso critério:
onde e . Assim.
Passo 4
Agora vamos calcular a máxima tensão cisalhante que de fato ocorre na peça:
Substituindo:
Passo 5
Agora é só substituir na equação da torção:
lembrando que utilizamos como a maior distância, logo o raio e é o momento polar de inércia calculado como:
Substituindo: