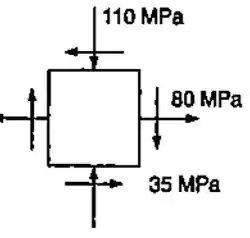
O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, com uma resistência ao escoamento na tração de . Determinar o coeficiente de segurança, em relação ao escoamento, usando: (a) o critério da máxima tensão de cisalhamento; (b) o critério da máxima energia de distorção.
Passo 1
Todos nós sabemos que existe um limite de carga para que as estruturas mecânicas não caiam em nossas cabeças. Esse limite é dado pela tensão aplicada a uma certo ponto da estrutura e pode ser definido segundo diversos critérios. Neste problema vamos utilizar dois deles o da máxima tensão de cisalhamento e o da máxima energia de distorção.
O critério da máxima tensão de cisalhamento é dado da seguinte forma:
Enquanto o critério da máxima energia de distorção é dado como:
Onde o valor do resultado dessa raíz quadrada deve estar dentro do limite fornecido no problema (normalmente a tensão limite de escoamento a tração ).
Mas essa questão não pede para ver se ocorrerá ou não ruptura, pede para calcular o coeficiente de segurança. E o que é isso? Coeficiente de segurança é um valor que diz quantas vezes a estrutura pode suportar a tensão máxima. Por exemplo, matar um mosquito com uma bazuka representa um alto coeficiente de segurança de que o mosquito vai morrer =D e isso é calculado como a razão entre a tensão de escoamento sobre a tensão máxima atuante no projeto (aquela que vem dos dois critérios já citados).
Obs: O coeficiente de segurança deve necessariamente ser maior do que 1.
Passo 2
O primeiro de tudo é construir o ciclo de Mohr, que vai ser da seguinte forma:
Repare que para a tensão é compressiva por isso é negativa, já para a tensão cisalhante ela é negativa por motivo de convenção apenas.
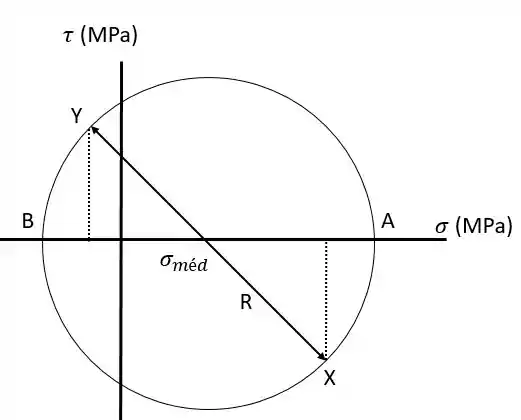
Perceba que a tensão cisalhante em e em são iguais, em módulo, e é positivo enquanto é negativo. Agora vamos achar o centro e o raio desse ciclo, respectivamente:
Como você pode ver é uma média simples e os termos e vem da imagem fornecida na questão:
Lembre-se que o sinal negativo representa uma tensão de compressão!
Sendo assim:
Agora falta só a tensão máxima de cisalhamento, que é igual ao raio do ciclo de Mohr e é fornecida como:
Pronto agora temos o ciclo de Mohr completo!
Passo 3
Com isso podemos responder a pergunta da letra A, utilizando a tensão máxima calculada , mas qual é a máxima tensão de cisalhamento admissível, se a a tensão de escoamento dada foi a de tração ()?
Simples! É só dividir essa tensão por dois:
Mas porque isso foi feito? Bom utilizamos o critério da máxima tensão cisalhante:
Além disso consideramos também que a tensão mínima de tração é nula! Daí chegamos a nossa relação:
Passo 4
Agora é só calcular o coeficiente de segurança, que neste caso vamos utilizar as tensões de cisalhamento:
obs: Não confunda o aplicado de fato ao componente, que é igual ao raio do ciclo de Mohr e chamado de neste exemplo, com o de escoamento que é intrínseco do material, chamado de .
Passo 5
Agora vamos resolver a letra B utilizando o critério da máxima energia de distorção:
Perceba que e são as tensões normais máxima e mínima, respectivamente. Isso vem lá do ciclo de mohr, pode dar uma olhadinha no passo 2 se quiser =D
Então a gente tem que achar esses valores, que é muito simples, só precisamos da tensão média e do raio:
Substituindo:
Como a nossa tensão máxima de escoamento é podemos calcular o coeficiente de segurança:
Resposta
a)
b)