Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 43
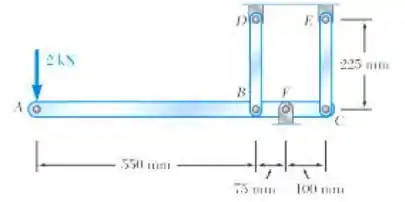
Cada uma das hastes BD e CE é feita de latão e tem área de seção transversal de 200mm². Determine a deflexão da extremidade A do elemento rígido ABC provocada pela ação de 2 kN.
Passo 1
E ai gurizada tudo belezinha??? Espero que sim!!! Para encontrarmos a deflexão pedida no enunciado é necessário que a gente faça nosso famoso diagrama de corpo livre, vem comigo :D
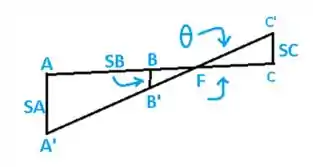
Sendo o a rotação do membro ABC, como mostrado então temos, os seguintes valores fornecidos no enunciado:
Mas,
Então temos que:
Desenhando o diagrama de corpo livre ABC:
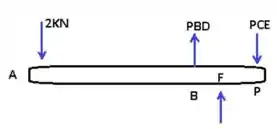
Consideramos que:
Isolando
Passo 2
Do corpo livre feito acima podemos realizar o somatório do momento em F, vejam :D
Ou
E a deflexão é dada por:
Resposta
Exercícios de Livros Relacionados
O comprimento do fio de aço CD de 3 32 in diâmetro foi ajustado de modo que, sem nenhuma força aplicada, existe um espaço de 1 16 i n entre a extremidade B da barra rígida ACB e um ponto de contato E.
Os elementos AB e BC são feitos de aço (E = 29x10 6 p s i ) e têm seção transversal com área de 0,80i n 2e0,64i n 2 , respectivamente. Para o carregamento mostrado, determine o alongamento do (a) elem
Cada uma das barras AB e CD é feita de alumínio ( E = 10,9x10 6 p s i e tem uma seção transversal com área de 0,2 i n 2 . Sabendo que elas suportam a barra rígida BC, determine o deslocamento do ponto
A barra ABC é feita de um alumínio para o qual E = 70G P a . Sabendo que P = 6 kN e Q = 42k N , determine o deslocamento de (a) ponto A e (b) ponto B.
O tubo de latão AB E = 105G P a tem área de seção transversal de 144 m m 2 e é ajustado com plugue em A. O tubo está conectado em B a uma placa rígida que, por sua vez, está conectada em C ao fundo de