Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 79
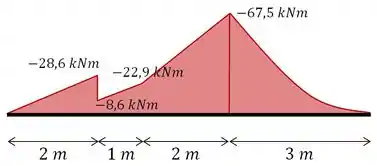
Determine os diagramas de força cortante e de momento fletor para a viga.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar os diagramas de força cortante e momento fletor para a viga considerando o carregamento dado. Então bora lá! Vamos começar representando a viga para facilitar a visualização do problema.
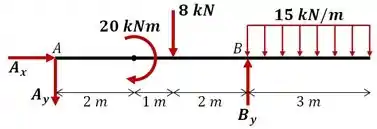
O primeiro passo é determinar as reações de apoio da viga. Para isso, vamos começar fazendo o equilíbrio de momentos em torno de :
Como não há forças da direção horizontal aplicadas, temos pelo equilíbrio de forças:
E na direção vertical:
Passo 2
Show de bola! Feito isso, vamos analisar as seções da esquerda para a direita usando a fórmula:
Começando pelo intervalo :
Ou seja, nesse intervalo atua uma cortante constante de . Para :
O que significa que a força constante negativa aumentou para . Para , temos:
Neste ponto tivemos um salto na cortante, que foi de para . E, finalmente, :
Como no intervalo atua uma força distribuída de , o gráfico nessa região é decrescente variando de até .
Passo 3
Agora ficou fácil fazer o diagrama de força cortante né? Precisamos apenas transferir esses dados para a viga de tal forma:
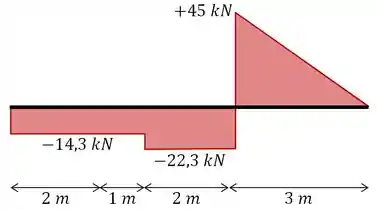
Passo 4
Até aqui tudo certo né? Vamos agora analisar a variação do momento ao longo da viga para cada intervalo utilizando a fórmula:
Lembrando que o momento é igual a zero em , e que a mudança no momento é igual à área do diagrama de força cortante.
Analisando o intervalo , o momento vai variar de forma decrescente de a:
No ponto , aplica-se um momento , gerando um salto de:
Para o intervalo , o momento volta a decrescer e chega em valendo:
Neste ponto é aplicada a força pontual de que altera a inclinação da reta que define o momento a partir deste ponto. Para o intervalo , temos:
Finalmente, no intervalo onde está atuando a força distribuída de , o momento vai variar seguindo uma curva quadrática com a concavidade virada para cima chegando em igual a zero:
Passo 5
Agora é só passar essas informações para a viga e temos o nosso diagrama de momento fletor!
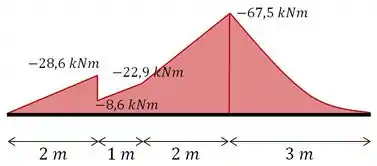
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 
Resposta
Diagrama de Força Cortante:
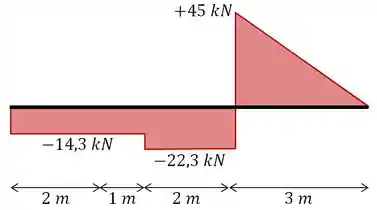
Diagrama de Momento Fletor:
