Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 27

Se o anel A se desloca com uma velocidade constante v A = { 3 i } m / s , determine a velocidade do anel B quando a barra AB está na posição mostrada. Suponha que a velocidade angular de AB é perpendicular a barra.

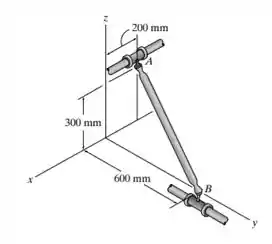
Passo 1

Utilizando a equação da velocidade relativa, temos

v B = v A + ω A B × r B / A

Como v B = v B j

ω A B = [ ( ω A B ) x i + ( ω A B ) y j + ( ω A B ) z k ]

r B / A = [ 0,2 i + 0,6 j - 0,3 k ] , então

v B j = 3 i + [ ( ω A B ) x i + ( ω A B ) y j + ( ω A B ) z k ] × ( 0,2 i + 0,6 j - 0,3 k )

v B j = [ 3 - 0.3 ( ω A B ) y - 0.6 ( ω A B ) z ] i + [ 0.3 ( ω A B ) x + 0.2 ( ω A B ) z ] j + [ 0.6 ( ω A B ) x - 0.2 ( ω A B ) y ] k

Passo 2

Equacionando nas direções i, j e k , temos

0 = 3 - 0.3 ( ω A B ) y - 0.6 ( ω A B ) z

v B = 0.3 ( ω A B ) x + 0.2 ( ω A B ) z

0 = 0.6 ( ω A B ) x - 0.2 ( ω A B ) y

Uma quarta equação pode ser obtida através do seguinte produto escalar

ω A B ⋅ r A / B = 0

[ ( ω A B ) x i + ( ω A B ) y j + ( ω A B ) z k ] ⋅ ( 0,2 i + 0,6 j - 0,3 k ) = 0

Resolvendo as equações iremos obter que a velocidade em B

v B = 1 m/s

Resposta

A velocidade será v B = 1 m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os carros A e B estão contornando as curvas com velocidades iguais 72 km/h. Determine a velocidade que A parece ter para um observador se deslocando e girando com o carro B para o instante representad
Um edifício alto está situado sobre o equador. O lado norte do edifício aloja um relógio de 12 horas comum cujo centro está a uma distância h acima do chão (que está aproximadamente ao nível do mar).
O caminhão de bombeiros está se deslocando para frente a uma velocidade de 60 km/h e está desacelerando na taxa de 3 m/s². Simultaneamente, a escada está sendo elevada e prolongada. No instante consid
Para o instante representado, a barra CB está girando no sentido anti-horário a uma taxa constante N = 4r a d / s , e seu pino A provoca uma rotação sentido horário do membro ranhurado ODE. Determine
O cursor montado sobre molas oscila no eixo de acordo com x = 0,04 s e n π t , onde x é expresso em metros e t é expresso em segundos. Simultaneamente a estrutura gira em torno do mancal em O com uma