Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 170

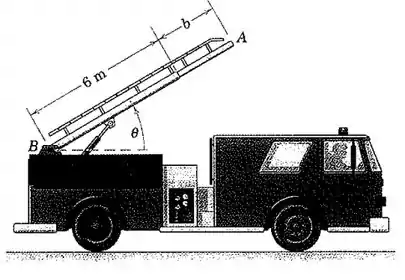
O caminhão de bombeiros está se deslocando para frente a uma velocidade de 60 km/h e está desacelerando na taxa de 3 m/s². Simultaneamente, a escada está sendo elevada e prolongada. No instante considerado, o ângulo θ = 30 ° e está aumentando na taxa constante de 10 graus/s. Nesse mesmo instante a extensão b da escada é de 1,5 m, com b ˙ = 0,6 m s e   b ¨ = - 0,3   m / s 2 . Determine para esse instante a aceleração da extremidade A da escada (a) em relação ao caminhão e (b) em relação ao solo.

Passo 1

Bom galera, vamos fazer um desenho do esquema e incluir as informações do enunciado para a visualização.

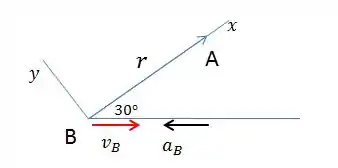
Muito importante nesta questão é colocar os eixos x-y sobre o eixo de rotação (a escada)!!!

Vamos agora parametrizar as variáveis. A velocidade e aceleração do caminhão podem ser escritas por:

v B = 60 3,6 c o s 30 °   i ^ - s e n 30 °   j ^ = 14,43 i ^ - 8,33 j ^   m / s

a B = 3 - c o s 30 °   i ^ + s e n 30 °   j ^ = - 2,6 i ^ + 1,5 j ^   m / s 2

A partir do vetor posição r , podemos encontrar a velocidade e aceleração da escada:

r = 6 + b = 7,5 i ^   m

r ˙ = b ˙ = v r e l = 0,6 i ^   m / s

r ¨ = b ¨ = a r e l = - 0,3 i ^   m / s 2

E enfim, vamos encontrar a velocidade angular e aceleração angular da escada a partir da variável θ :

θ ˙ = ω = 10 g r a u s s × π 180 r a d g r a u = 0,175 k ^   r a d / s

θ ¨ = α = 0

Passo 2

Nesta etapa, vamos usar a equação da aceleração relativa.

  1. Para a extremidade da escada. Isso quer dizer que nosso referencial é o ponto B.

    2. a A = a B + α × r + ω × ω × r + 2 ω × v r e l + a r e l

    a A = 0 + 0 - 0,175 2 7,5 i ^ + 2 0,175 k ^ × 0,6 i ^ - 0,3 i ^

    a A = - 0,53 i ^ + 0,21 j ^   m / s 2

  2. Em relação ao chão. Isso quer dizer que deve levar em consideração a aceleração do caminhão.

a A = a B + α × r + ω × ω × r + 2 ω × v r e l + a r e l

a A = - 2,6 i ^ + 1,5 j ^ + 0 - 0,175 2 7,5 i ^ + 2 0,175 k ^ × 0,6 i ^ - 0,3 i ^

a A = - 3,13 i ^ + 1,71 j ^   m / s 2

Resposta

  1. a A = - 0,53 i ^ + 0,21 j ^ m s 2
  2. a A = - 3,13 i ^ + 1,71 j ^ m s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante quando θ = 90 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 15r a d / s e aceleração angular ω ˙ 1 = 3r a d / s 2 . Simultaneamente, os painéis solares giram com um
Se a estrutura gira com uma velocidade angular constante ω p = - 10 kr a d / s e a engrenagem horizontal B gira com uma velocidade angular constante ω B = 5 kr a d / s , determine a velocidade angular
No instante mostrado, o motor gira em torno do eixo z com uma velocidade angular ω 1 = 3m / s e aceleração angular ω ˙ 1 = 1,5r a d / s 2 . Simultaneamente, o eixo O A gira com uma velocidade angular
No instante θ = 30 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 29r a d / s , e tem uma aceleração angular ω ˙ 1 = 5r a d / s 2 . Simultaneamente, os painéis solares giram com
Quando a barra AB está na posição mostrada, o anel A se desloca com uma velocidade v A = { 3 i } m/s e aceleração a A = { 0,5 i } m/s2, determine a aceleração do anel B nesse instante. Suponha que a v