Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 175

Um edifício alto está situado sobre o equador. O lado norte do edifício aloja um relógio de 12 horas comum cujo centro está a uma distância h acima do chão (que está aproximadamente ao nível do mar). Desenvolva expressões para a velocidade e a aceleração da extremidade A do ponteiro das horas às 12 horas quando medidas a partir de um sistema de coordenadas sem rotação no centro da Terra. Assuma que o sentido positivo do eixo x é a partir do centro da Terra radialmente para fora apontando para o edifício e que o do eixo z aponta para o norte. O ponteiro das horas tem um comprimento l e executa duas rotações completas em relação ao relógio durante uma rotação completa da Terra. O raio e a velocidade angular da Terra são R e ω .

Passo 1

Bom pessoal, a primeira coisa que devemos fazer nesse exercício é um esquema para visualizar o que o enunciado fala. Usando as referências dos eixos como citado, z aponta para o norte (saindo da tela), x está na direção do edifício. Temos que:

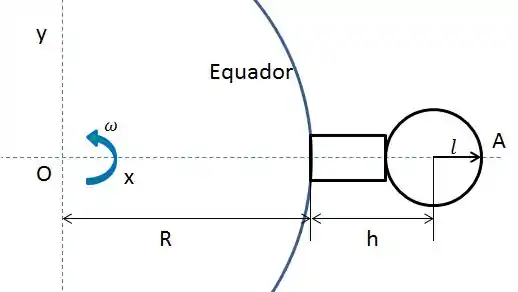
Esta é a parte mais difícil da questão! Vamos para as contas agora!

O relógio dá 2 voltas quando a Terra da 1 volta. Então:

ω r = 2 ω

Onde ω r é a velocidade angular do relógio e ω é a velocidade angular da Terra.

A velocidade de A medida em relação ao centro do relógio vale:

v r e l = - l ω r j ^ = - 2 l ω j ^

Agora, vamos calcular a velocidade de A em relação ao centro da Terra:

v A = v O + ω k ^ × R + h + l i ^ - 2 l ω j ^

v A = R + h - l ω j ^   m / s

Passo 2

Pronto! Agora vamos calcular a aceleração relativa entre a extremidade do ponteiro A e o centro da Terra O.

a A = a O + α × r A O + ω × ω × r A O + 2 ω × v r e l + a r e l

Do mesmo modo que calculamos v r e l vamos também calcular a r e l , que é a aceleração do ponteiro em relação ao centro do relógio:

a r e l = - l ω r 2 = - 4 l ω 2 i ^   m / s 2

Voltando à equação:

a A = 0 + 0 - ω 2 R + h + l i ^ + 2 ω k ^ × - 2 l ω j ^ - 4 l ω i ^

a A = - ω 2 R + h + l i ^ + 4 l ω 2 i ^ - 4 l ω 2 i ^

a A = - ω 2 R + h + l i ^   m / s 2

Resposta

a A = - ω 2 R + h + l i ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, o helicóptero está se deslocando para cima com uma velocidade v H = 1,2m / s e tem uma aceleração a H = 0,6m / s 2 . No mesmo instante, a fuselagem H , não o rotor horizontal, gi
No instante mostrado, o helicóptero está se deslocando para cima com uma velocidade v H = 1,2m / s e tem uma aceleração a H = 0,6m / s 2 . No mesmo instante, a fuselagem H , não o rotor horizontal, gi
No instante mostrado, a estrutura da escavadeira se desloca para frente na direção y com uma velocidade de 2m / s e uma aceleração de 1m / s 2 , enquanto a cabine gira em torno do eixo z com uma veloc
No instante quando θ = 90 ° , o corpo do satélite se desloca na direção x com uma velocidade v O = 500 im / s e aceleração a o = 50 i m / s 2 . Simultaneamente, o corpo também gira com uma velocidade
O cone rola em um círculo e gira em torno do eixo z a uma taxa constante ω z = 8r a d / s . Determine a velocidade e a aceleração angular do cone se ela rola sem deslizar. Além disso, qual é a velocid