Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 25

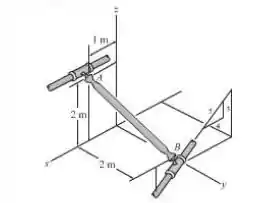
Se o anel A se desloca com uma velocidade constante v A = 5 i   m / s , determine a velocidade do anel B quando a barra A B está na posição mostrada. Suponha que a velocidade angular de A B é perpendicular à barra.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos pede a velocidade do anel B quando a barra A B está na posição mostrada.

Vamos às analises:

v B = 4 5 v B i - 3 5 v B k

v A = 5 i

ω A B = ω x i + ω y j + ω z k

r B / A = - 1 i + 2 j - 2 k

Temos então que:

v B = v A + ω A B × r B / A

4 5 v B i - 3 5 v B k = 5 i + ω x i + ω y j + ω z k × - 1 i + 2 j - 2 k

Para resolver produto vetorial, temos que ter cuidado com quem multiplica quem primeiro. Por exemplo:

i × j ≠ j × i

Aqui estão todos os produtos dos vetores unitários:

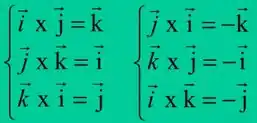
Passo 2

Portanto:

4 5 v B i - 3 5 v B k = 5 i + ω x i + ω y j + ω z k × - 1 i + 2 j - 2 k

Vamos encontrar cada termo da equação de v B , para melhorar a organização dos cálculos:

ω A B × r B / A = ω x i + ω y j + ω z k × - 1 i + 2 j - 2 k

ω A B × r B / A = i j k ω x ω y ω z - 1 2 - 2

ω A B × r B / A = - 2 ω y i - 1 ω z j + 2 ω x k - 2 ω z i - 2 ω x j - 1 ω y k

ω A B × r B / A = - 2 ω y - 2 ω z i + - 1 ω z + 2 ω x j + 2 ω x + 1 ω y k

Juntando tudo temos:

4 5 v B i - 3 5 v B k = 5 i + - 2 ω y - 2 ω z i + - 1 ω z + 2 ω x j + 2 ω x + 1 ω y k

Passo 3

Agora vamos montar um sistema para cada componente:

4 5 v B i = 5 i + - 2 ω y - 2 ω z i

0 j = - 1 ω z + 2 ω x j

- 3 5 v B k = 0 k + 2 ω x + 1 ω y k

É possível observar que temos 3 equações e 4 variáveis. Portanto, precisamos de uma quarta equação dada por:

ω A B ⋅ r B / A = 0

ω x i + ω y j + ω z k ⋅ - 1 i + 2 j - 2 k = 0

- 1 ω x + 2 ω y - 2 ω z = 0

Passo 4

Relacionando as 4 equações, temos que:

ω x = 1 , 667   r a d / s

ω y = 4,167   r a d / s

ω z = 3,333   r a d / s

v B = - 12,5   m / s

Logo:

v B = 4 5 - 12,5 i - 3 5 - 12,5 k

v B = - 10 i + 7,5 k   m / s

Resposta

v B = - 10 i + 7,5 k   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, a cabine da escavadeira gira em torno do eixo z com uma velocidade angular constante ω z = 0,3r a d / s . No mesmo instante θ = 60 ° , e a lança O B C tem uma velocidade angular
No instante mostrado, o eixo gira com uma velocidade angular ω p = 6r a d / s e uma aceleração angular ω ˙ p = 3r a d / s 2 . No mesmo instante, o disco gira em torno de seu eixo com uma velocidade an
O disco A gira a uma velocidade angular constante de 10r a d / s . Se a barra B C está ligada ao disco e ao anel por juntas esféricas, determine a velocidade do anel B no instante mostrado. Além disso
Resolva o exemplo 20.5 fixando os eixos x , y , z àbarra B D de maneira que Ω = ω 1 + ω 2 . Neste caso, o anel parece se deslocar apenas radialmente para fora ao longo de B D ; por conseguinte,Ω x y z
A placa triangular A B C está apoiada em A por uma junta esférica e em C pelo plano x - z . O lado A B encontra-se no plano x - y . No instante θ = 60 ° , θ ˙ = 2r a d / s , θ ¨ = 3r a d / s 2 e o pon