Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 13
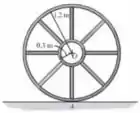
Se o anel grande, o anel pequeno e cada um dos arcos têm uma massa de 50 kg, 7,5 kg e 10 kg, respectivamente, determine o momento de inércia de massa da roda em relação a um eixo perpendicular à página e passando pelo ponto A.
Passo 1
A roda pode ser subdividida em duas partes, sendo elas no arco menor com raio de 0,3 m e em uma outra parte circular, mas retirando a parte central. Através da figura conseguimos encontrar o centro de massa da roda, sendo ela igual a a partir do ponto .
Passo 2
Vamos descobrir o momento de inércia que é perpendicular à página e passa pelo centro . Com isso,
Passo 3
Bom, o momento de inércia de massa da roda pode ser calculado pelo teoremos dos eixos paralelos, , onde .
Agora ficou fácil calcular , pois ele será .
Resposta
Exercícios de Livros Relacionados
O cilindro de 100 kg rola sem deslizar sobre o plano horizontal. Determine a aceleração de seu centro de massa e sua aceleração angular.
A barra fina uniforme de 60 kg está inicialmente em repouso sobre um plano horizontal liso quando as forças são aplicadas. Determine a aceleração do centro de massa da barra e a aceleração angular da
A barra fina de 12 kg está presa com pino ao rolete pequeno A que desliza livremente ao longo da ranhura. Se a barra é solta do repouso em θ = 0 ° , determine a aceleração angular da barra e a acelera
A esfera de 20 kg rola para baixo sobre o plano inclinado sem deslizar. Determine a aceleração angular da esfera e a aceleração de seu centro de massa.
A roda de 20 kg tem um raio de giração em relação a seu centro O de k O = 300m m . Quando a roda é submetida ao momento de binário, ela desliza na medida em que rola. Determine a aceleração angular da