Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 126

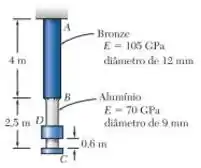
O anel D é liberado do repouso na posição mostrada, e o seu movimento é interrompido por uma pequena placa fixada à extremidade C da barra vertical A B C . Determine a massa do anel para o qual a tensão normal máxima na parte B C é de 125   M P a .

Passo 1

Fala aí, galera. Tudo bele? Vamos praticar mais mecânica pra craque.

Neste exercício temos que determinar a massa do anel para o qual a tensão normal máxima na parte B C é de 125   M P a . Para isso, vamos começar determinando a área da seção transversal desta porção:

A B C = π 4 d 4 A B C = π 4 0,009 4 A B C = 63,617 × 10 - 6   m 2

E também, vamos utilizar a relação da tensão de escoamento a fim de determinarmos a carga submetida à barra. Ela é dada pela razão da carga aplicada pela área da seção, portanto:

σ = P A = 125 × 10 9 = P 63,617 × 10 - 6 P = 7952   N

Assim, a energia de deformação para esta porção da barra vai ser:

U B C = P 2 L B C 2 E B C A B C = 7952 2 2,5 2 70 × 10 9 63,617 × 10 - 6 U B C = 11 , 750   J

Em seguida, vamos fazer o mesmo para a haste A B . Temos que a área da seção transversal do cilindro é dada por:

A A B = π 4 d 4

Substituindo:

A A B = 113,907 × 10 - 6   m 2

E então, a energia de deformação para a porção A B da barra vai ser:

U A B = P 2 L A B 2 E A B A A B U A B = 7952 2 4 2 105 × 10 9 113,907 × 10 - 6 U A B = 10,574

Portanto, vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação para cada haste. Fica assim:

U = U A B + U B C = 17,750 + 10,574 U = 28,324   J

Passo 2

Agora que encontramos a energia de deformação da barra, podemos determinar a deformação correspondente. Fica assim:

U = 1 2 P ∆ 28,324 = 1 2 7952 ∆ ∆ = 7,12 × 10 - 3

E também, vamos determinar a altura de queda do anel:

h = 0,6 + 7,12 × 10 - 3 h = 0,60712   m

Por fim, podemos determinar a massa do anel através do trabalho da força peso. Temos:

W h = m g h = U m = U g h = 28,324 9,81 0,60712 m = 4,76   k g

É isso, galera Bora pra próxima?

Resposta

m = 4,76   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando E = 75G P a , determinar:a energia de deformação da barra de alumínio A B C , quando a = 1,2m ;a correspondente densidade de energia de deformação nas porções A B e B C da barra.
Usando E = 200G P a , determinar:a energia de deformação da barra de aço A B C , quando P = 60k N ;a correspondente densidade de energia de deformação nas porções A B e B C da barra.
O diagrama tensão-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de um corpo de prova de uma liga de alumínio. Usando E = 72G P a , determinar:o módulo de res
O diagrama carga-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de um corpo de prova de uma liga de alumínio. Sabendo-se que a área da seção transversal do C
Uma porção de uma barra de aço quadrada, de 22m m de lado, foi usinada produzindo um cilindro de diâmetro 22m m , como mostrado. Sabendo-se que a tensão normal admissível do aço é σ a d m = 150M P a e