Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 1

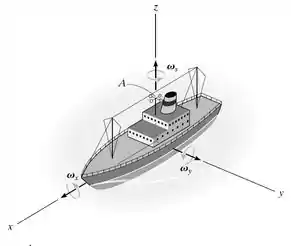
O anemômetro localizado no barco A gira em torno de seu próprio eixo a uma taxa w s , enquanto o barco rola em torno do eixo x com taxa de w x e em torno do eixo y com taxa de w y . Determine a velocidade angular e a aceleração angular do anemômetro no instante em que o barco está nivelado como mostrado. Suponha que as intensidades de todas as componentes da velocidade angular são constantes e que o movimento de rolamento causado pelo mar é idependente nas direções x e y.

Passo 1

A velocidade angular medida a partir dos eixos x,y e z , é simplesmente a soma vetorial das suas componentes. Desse modo:

ω = ω x i + ω y j + ω z k

Considere Ω = ω x i + ω y j

Passo 2

Sabendo que ω x e ω y são idependentes entre si, eles não variam a sua direção e magnitude, assim a aceleração angular será:

α = ω ˙ = ω ¨ x y z + ω x + ω y × ω z

α = 0 + ω x i + ω y j × ω z k

α =   ω y ω x i -   ω x ω z j

Resposta

De acordo com os passos 1 e 2 e as considerações feitas, a velocidade angular e a aceleração angular do anemômetro no instante em que o barco está nivelado serão respectivamente :

ω = ω x i + ω y j + ω z k

α =   ω y ω x i -   ω x ω z j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa triangular A B C está apoiada em A por uma junta esférica e em C pelo plano x - z . O lado A B encontra-se no plano x - y . No instante θ = 60 ° , θ ˙ = 2r a d / s e o ponto C tem as coordenad
A barra A B está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A tem uma velocidade v A = 1,5 im / s e uma aceleração a A = 0,2 im / s 2 no instante mostrado, determine a acel
Se a manivela B C está girando com uma velocidade angular ω B C = 6r a d / s e uma aceleração angular ω ˙ B C = 1,5r a d / s 2 , determine a aceleração do anel A nesse instante. Suponha que a velocida
No instante mostrado, a cabine da escavadeira gira em torno do eixo z com uma velocidade angular constante ω z = 0,3r a d / s . No mesmo instante θ = 60 ° , e a lança O B C tem uma velocidade angular
No instante mostrado, o eixo gira com uma velocidade angular ω p = 6r a d / s e uma aceleração angular ω ˙ p = 3r a d / s 2 . No mesmo instante, o disco gira em torno de seu eixo com uma velocidade an