Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 184
A barra gira no sentido anti-horário com uma velocidade angular constante de . Através de meios mecânicos, o anel move-se ao longo da barra com uma velocidade escalar de , onde é dado em segundos. Se quando , determine as intensidades da velocidade e aceleração do anel quando .
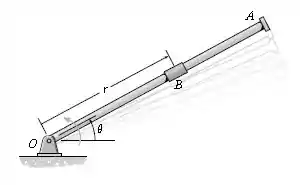
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O enunciado nos pede as intensidades da velocidade e aceleração do anel quando .
Do enunciado, temos que quando , logo:
Integrando, temos:
Passo 2
Quando , temos:
E:
Queremos:
E:
Passo 3
Vamos às analises:
Como é constante, sabemos que a derivada de uma constante é zero, portanto:
Passo 4
Sabemos que:
A magnitude da velocidade será:
Passo 5
Para a aceleração, teremos que a componente é:
A componente é dada por:
Logo:
Resposta
Exercícios de Livros Relacionados
Uma partícula se desloca em uma trajetória circular de 0,3m de raio. Calcule o módulo a da aceleração da partícula(a) se a sua velocidade é constante em 0,6m / s e(b) se a sua velocidade é 0,6m / s ,
Uma sonda espacial deve ser colocada em uma órbita circular de 5600 milhas de raio em torno do planeta Vênus em um plano especificado. Quando a sonda atinge A, o ponto de sua trajetória original mais
Para a sonda espacial do Problema 12.106, sabe-se que r A = 9,3 x10³ mi e que a velocidade da sonda é reduzida para 20.000 ft/s, conforme ela passa por A. Determine (a) a distância do centro de Vênus
A espaçonave Clementine descreveu uma órbita elíptica de altitude mínima hA = 400 km e altitude máxima de hB = 2.940 km acima da superfície da lua. Sabendo que o raio da lua é 1737 km e a massa da lua
Uma sonda espacial em uma órbita baixa da Terra é inserida em uma órbita de transferência elíptica para o planeta Vênus. Sabendo que a massa do sol é 332,8 x 10³ vezes a massa da terra e assumindo que