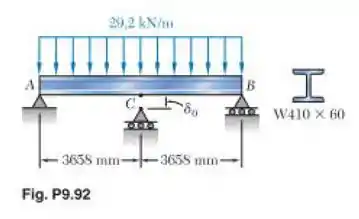
Antes de ser aplicado o carregamento de 29,2 kN/m, havia uma folga entre a viga W410 X 60 e o apoio em C. Sabendo que E = 200 GPa, determine a reação em cada apoio depois de ser aplicada a força uniformemente distribuída.

Tá legal! Vamos começar esse exercício encontrando o momento de inércia da nossa viga, para isso vamos lá no apêndice C, de onde teremos:

Vamos aproveitar e calcular o valor do termo EI, que também usaremos lá na frente. Então teremos:

Agora nós vamos dividir o carregamento na viga em 2, no primeiro caso consideraremos somente o carregamento distribuído aplicado a viga e depois iremos considerar somente a força de apoio em C. Então para o primeiro caso, temos que a deflexão no ponto C será dada pelo caso 6 do apêndice D, onde temos:

Agora, no segundo caso, teremos somente a força de apoio C aplicada no meio da viga, nesse caso, a deflexão máxima será no ponto C e será dada pelo caso 4 do apêndice D, onde teremos:

Então, agora sabemos que a deflexão total na viga será igual a folga , só que no sentido oposto, ou seja:

Substituindo as expressões que encontramos e lembrando que a deflexão 1 é para baixo e a 2 é para cima, teremos:

Substituindo os valores conhecidos, teremos:

Agora, para encontrar o valor da reação em A, vamos aplicar o somatório de momento em relação ao ponto B, então teremos:

E, por fim, para encontrar a reação no ponto B, vamos aplicar o somatório de forças na direção vertical, de onde teremos:

Shoow! Terminamos mais um, valeeu!