Após completar sua missão de exploração na Lua, os dois astronautas da tripulação de um módulo de excursão lunar Apollo iriam preparar o retorno ao módulo de comando que orbitava na Lua a uma altitude de . Eles acionariam o motor do módulo lunar, levariam-no ao longo de uma trajetória curva até o ponto , a acima da superfície da Lua, e desligariam o motor. Sabendo que o módulo lunar movia-se naquele instante em uma direção paralela à superfície da Lua e que, então, seguiria livre ao longo de uma trajetória elíptica para reencontrar o módulo de comando em , determine (a) a velocidade do módulo lunar após o desligamento do motor, (b) a velocidade relativa com a qual o módulo de comando se aproximaria do módulo lunar em . (O raio da Lua é de e sua massa é 0,0123 vezes a massa da Terra.)
Passo 1
Oi, pessoal! Tudo bem? Vamos à resolução do problema!!
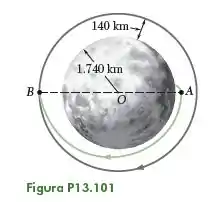
Observe que, o módulo de comando está no ponto B. O enunciado e a figura nos fornecem como dados:
Nosso dever é determinar a velocidade do módulo lunar após o desligamento do motor , e a velocidade relativa com a qual o módulo de comando se aproximaria do módulo lunar em , . Como temos as altitudes dos pontos e e o raio da lua, vamos incialmente calcular e .
Aplicando o princípio da conservação do momento angular:
Passo 2
Calculando a energia cinética e potencial.
Ponto A:
Aplicando agora a Eq. 13.17, usada para a energia potencial quando a variação da força da gravidade não pode ser desprezada:
O produto , pode ser expresso conforme a Eq. 12,29:
Sabemos que,
E sendo
Substituímos os valores na equação para obtermos :
Substituindo em :
Ponto B:
Aplicamos a Eq. 13.17 para obter a energia potencial:
Passo 3
Em posse das energias cinética e potencial, vamos aplicar o princípio da conservação da energia:
Sabemos que
Então,
Passo 4
Vamos agora encontrar a velocidade relativa com a qual o módulo de comando se aproximaria do módulo lunar em .
Temos que,
Substituindo o valor encontrado para :
O módulo de comando está em órbita circular. O valor da velocidade inicial correspondente a uma órbita circular é encontrado através da Eq. 12.44:
Calculando a velocidade relativa , temos: