O carro de 2 Mg aumenta a sua velocidade uniformemente a partir repouso para 25m/s em 30 s subindo a estrada. Determine a potencia máxima que deve ser fornecida pelo motor que opera com uma eficiencia de ()=0,8. Determine também a potencia média fornecida pelo motor.

Passo 1
Utilizando a 2º lei de Newton para encontrar a força F
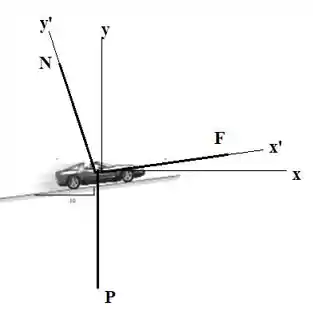
A aceleração pode ser calculada pela equação da velocidade para MRUV
Passo 2
Então substituindo a aceleração em (1)
Então a potencia máxima será
A potencia média será
Resposta
A potencia máxima e média útil serão, respectivamente, 113kW e 56.5kW