Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 164

Mostre que para a bola que atinge uma superfície fixa sem atrito, α > θ . Mostre que a percentagem perdida de energia cinética devido ao impacto é 100 1 - e 2 cos 2 ⁡ θ .

Passo 1

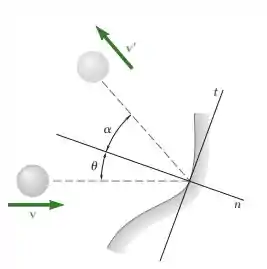
Fala aí, galerinha do Responde aí. Beleza? Bora pra mais uma questão de dinâmica. Sabemos que o momento na direção t é conservado, já que não há atrito. Logo:

m v t = m v t ' v sin ⁡ θ = v ' sin ⁡ α   ( 1 )

Em seguida, vamos utilizar a relação do coeficiente de restituição na direção n :

v n e = v n ' v cos ⁡ θ e = v ' cos ⁡ α   ( 2 )

E então, dividindo a equação ( 1 ) pela equação ( 2 ) , temos:

v sin ⁡ θ v cos ⁡ θ e = v ' sin ⁡ α v ' cos ⁡ α e = tan ⁡ θ tan ⁡ α

Com isso, encontramos o valor do coeficiente de restituição e, como sabemos que e   está no intervalo 0 < e < 1 , podemos confirmar o que o enunciado nos disse, pois:

tan ⁡ α > tan ⁡ θ Logo:

α > θ

Passo 2

Para encontramos a porcentagem de energia cinética perdida, podemos elevar as equações que encontramos anteriormente ao quadrado:

v 2 sin 2 ⁡ θ + e 2 cos 2 ⁡ θ = v ' 2

Agora, vamos pegar essa relação e substituir na equação da variação de energia cinética para podermos comprovar o que se pede:

∆ T = 1 2 m v 2 - v ' 2

Substituindo: ∆ T = 1 2 m v 2 cos 2 ⁡ θ 1 - e 2 % e n e r g i a   p e r d i d a = 100 1 - e 2 cos 2 ⁡ θ

É isso, galera, conseguimos provas as afirmações propostas. Bora zerar esse livro!

Resposta

α > θ

% e n e r g i a   p e r d i d a = 100 1 - e 2 cos 2 ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que o raio r da órbita de uma lua de um determinado planeta pode ser determinado a partir dos raios R do planeta, da aceleração da gravidade na superfície do planeta e do tempo necessário para
Para a partícula do Problema 12.76 mostre (a) que a velocidade da partícula e a força central F são proporcionais à distância r da partícula ao centro de força O, (b) que o raio de curvatura do caminh
Uma espaçonave é colocada em uma órbita polar em torno do planeta Marte a uma altitude de 380 km. Sabendo que a densidade média de Marte é 3,94 Mg / m³ e que o raio de Marte é 3397 Km, determine (a) o
Uma espaçonave de 600 kg é colocada primeiramente em uma órbita circular em torno da Terra a uma altitude de 4.500 km e, então, transferida para uma órbita circular em torno da Lua. Sabendo que a mass
A haste 0A oscila cerca de 0 em um plano horizontal. O movimento do colar B de 5 lb é definido pelas relaçõesr = 10 / ( t + 4 ) and θ = ( 2 / π ) s i n ⁡ π t , onde r é expresso em pés, t em segundos