Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 116

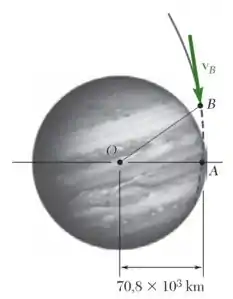
Ao aproximar-se do planeta Júpiter, uma nave espacial libera uma sonda que entra na atmosfera do planeta no ponto B a uma altitude de 450 km acima da superfície do planeta. A trajetória da sonda é uma hipérbole de excentricidade 1,031. Sabendo que o raio e a massa de Júpiter são 71,492 103 km e 1,9 1027 kg, respectivamente, e que a velocidade vB da sonda em B forma um ângulo de 82,9° com a direção AO, determine (a) o ângulo AOB, (b) a velocidade escalar vB da sonda em B.

Passo 1

E ai pessoal tudo certinho? O enunciado pede que a gente determine (a) o ângulo AOB, (b) a velocidade escalar vB da sonda em B.

Primeiro notamos r B = 71.492 × 10 3 = 450 k m = 71.942 × 10 3 k m

  1. Nós temos [Eq. (12.39)] do livro

1 r = G M j h 2 1 + ε   c o s θ

No A, θ = 0 :

1 r A = G M j h 2 1 + ε

ou

h 2 G M j = r A 1 + ε

Passo 2

No B, θ = θ B = ∡ A O B :

1 r B = G M j h 2 1 + ε   c o s θ B

ou

h 2 G M j = r B 1 + ε   c o s θ B

Então

r A 1 + ε = r B 1 + ε   c o s θ B

c o s θ B = 1 ε r A r B + 1 + ε   - 1 = 1 1.031 70.8 × 10 3 k m 71.942 × 10 3 k m + 1 + 1.031   - 1 = 0.96873

θ B = 14.3661 °

Passo 3

(b)De cima

h ² = G M j r B 1 + ε   c o s θ B

onde

h = 1 m r B   ×   m v B = r B v B s e n ∅

∅ = θ B + 83.9 ° = 97.2661 °

Então

r B v B s e n ∅ 2 =   G M j r B 1 + ε   c o s θ B

ou

v B = 1 s e n ∅ G M r B 1 + ε   c o s θ B   1 / 2 = 1 s e n   97.2661 °

66.73 × 10 - 12 m 2 / k g ∙ s ² × 1.9 × 10 27 k g 71.942 × 10 6 m × [ 1 + 1.031 0.96873 ] 1 / 2

Resposta

a )   ∡ A O B = 14.37 °

b )   v B = 59.8 k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro está viajando a uma velocidade escalar de 30m / s . O motorista, então, aciona os freios em A e, assim, reduz a velocidade escalar do carro a uma razão de a t = - 0,08 vm / s 2 , onde v é dado
Quando o carro chega ao ponto A, ele tem velocidade escalar de 25m / s . Se os freios são acionados, sua velocidade escalar é reduzida em a t = - 1 4 t 1 2m / s 2 . Determine a intensidade da aceleraç
Quando o carrinho de montanha-russa está em B, ele tem uma velocidade escalar de 25 m/s, a qual está aumentando em a t = 3m / s 2 . Determine a intensidade da aceleração do carrinho da montanha-russa
Um avião voa ao longo da trajetória circular horizontal AB em 60s . Se a sua velocidade escalar no ponto A é 120m / s , que diminui a uma razão de a t = - 0,03 tm / s 2 , determine a intensidade da ac
Determine a intensidade da aceleração do avião durante a curva. Ele voa ao longo da trajetória circular horizontal AB em 40s , enquanto mantém uma velocidade escalar constante de 90m / s .