Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 128
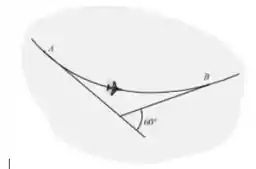
Um avião voa ao longo da trajetória circular horizontal AB em . Se a sua velocidade escalar no ponto A é , que diminui a uma razão de , determine a intensidade da aceleração do avião quando ele chegar ao ponto B.
Passo 1
Para podermos determinar a intensidade da aceleração, precisamos calcular as componentes tangencial e a componente normal da aceleração. E para calcularmos a componente normal, precisamos determinar o raio de curvatura. Este resultado será obtido a partir da geometria do problema, pois o comprimento do arco de uma circunferência é:
Portanto, para calcularmos , precisamos obter antes e . Para calcularmos o primeiro, vamos utilizar as equações da cinética. Já para obter o ângulo, vamos utilizar relações geométricas!
Passo 2
Começaremos determinando as equações que governam a velocidade a posição do avião. Sendo assim, temos:
Já para a posição, temos:
Passo 3
O avião percorre o comprimento em . Sendo assim,
Para calcularmos o raio de curvatura, vamos observar a geometria do problema abaixo.
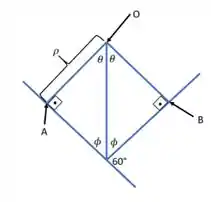
Pela figura sabemos que:
E, no triângulo retângulo,
Como , temos . Portanto, o raio de curvatura é:
Passo 4
Antes de calcularmos a aceleração, precisamos determinar a velocidade do avião após os . Para isto, vamos substituir este valor na equação obtida no Passo 2! Portanto,
Passo 5
Agora podemos calcular a aceleração. Começando pela componente normal, temos:
Já a componente tangencial é dada por:
Por fim, a intensidade da aceleração do avião é: