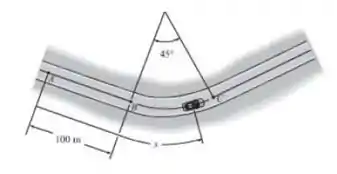
O carro está viajando a uma velocidade escalar de . O motorista, então, aciona os freios em A e, assim, reduz a velocidade escalar do carro a uma razão de , onde é dado em . Determine a aceleração do carro pouco antes de ele chegar ao ponto C da curva circular. O carro leva para viajar de A para C.

Começaremos determinando a função da velocidade. Sendo assim, temos:

Portanto, após , temos:

Agora, vamos determinar o comprimento do arco , para que possamos determinar o raio de curvatura. Utilizando as equações da cinética, temos:

Após , o carro percorreu a seguinte distância:

Entretanto, esta distância é toda a distância percorrida pelo carro, seja na curva ou no trecho retilíneo. Sendo assim, o comprimento do arco é:

E o raio de curvatura será dado por:

Agora podemos calcular a componente normal da aceleração. Desta forma, temos:

E a componente tangencial da aceleração é:

Portanto, a intensidade da aceleração é: