Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 129
Quando o carrinho de montanha-russa está em B, ele tem uma velocidade escalar de 25 m/s, a qual está aumentando em . Determine a intensidade da aceleração do carrinho da montanha-russa nesse instante e o ângulo de direção que ela faz com o eixo .
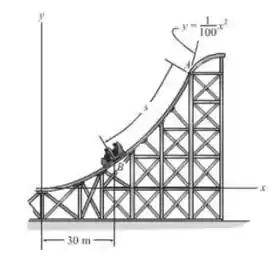
Passo 1
Precisamos determinar a intensidade da aceleração, e o ângulo que faz com o eixo . Como já nos foi dado a sua componente tangencial, só precisamos calcular a sua componente normal. Mas aí a gente se questiona: e cadê o raio de curvatura? Este é o ponto mais difícil da questão. Para calcularmos o raio de curvatura, será necessário utilizarmos a seguinte equação:
Obtido a função para o raio da curvatura, basta substituir o valor de que obtemos o raio. Depois disto, basta utilizar as equações da cinemática para determinarmos as componentes da aceleração. Agora, a questão também nos pede o ângulo que a aceleração faz com o eixo . Este dado será um pouco trabalhoso de obtermos, pois precisaremos fazer uma análise geométrica.
Passo 2
Antes de calcularmos a componente normal, precisamos determinar o raio de curvatura. Para isto, utilizaremos a fórmula do Passo 1. Primeiramente, derivaremos a função que governa a nossa curva duas vezes. Sendo assim:
Substituindo na fórmula do raio de curvatura, temos:
Quando , temos:
Passo 3
Calculando a componente normal, temos:
Portanto, a intensidade da aceleração é:
Passo 4
Agora, só nos falta determinar o ângulo. Para isto, vejamos a figura abaixo, em que detalha os ângulos formados pelos vetores da aceleração.
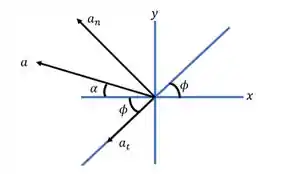
O ângulo que queremos determinar é o . E Sabemos que:
A questão é quem é este ângulo . Ele é a inclinação da reta tangente a função no ponto , isto é:
Portanto,