Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 80
A área mostrada é girada de 360 graus em torno do eixo . Determine o volume do corpo resultante, que é uma esfera que tem uma parte significativa removida.
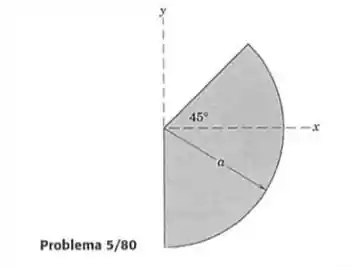
Passo 1
Vamos primeiro ver o problema com base numa visão melhor da imagem abaixo!
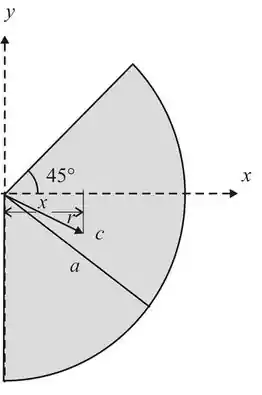
Passo 2
Galera, essa é bem tranquila, basta pegarmos da tabela D/3, com um
Resposta
Exercícios de Livros Relacionados
Determine por integração direta os centroides das áreas a seguir.v
Determine o volume e a área da superfície do sólido obtido pela rotação da área da área do problema erm torno de ( a ) da linha y = 60 m m , ( b ) do eixo y .
Determine por integração direta os centroides das áreas a seguir.
Um arame homogêneo é dobrado na forma mostrada na figura. Determine por integração direta a coordenada x de seu centroide. Expresse sua resposta em termos de A .
Determine o volume e a área da superfície do sólido obtido pela rotação da área da área do problema erm torno de ( a ) da linha x = 240m m , ( b ) do eixo y .