Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 205

205- Determine as coordenadas x e y do centroide da área sombreada.

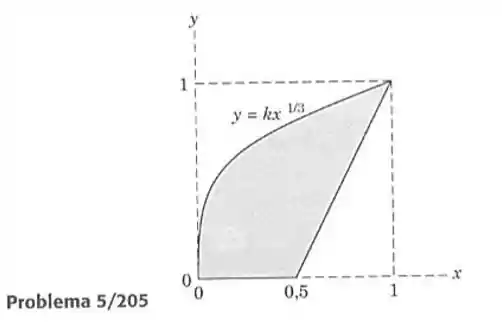
Passo 1

Fazendo pelo método da somatória das linhas temos nós teremos o seguinte gráfico para resolver:

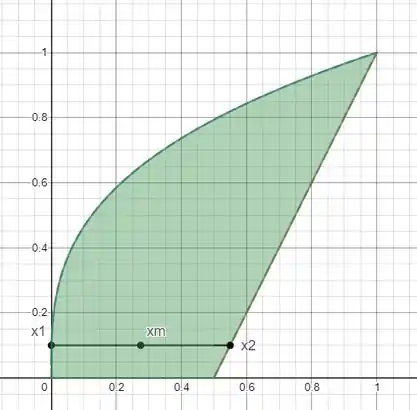
Onde a reta que passa pelos pontos ( 0.5 ; 0 ) e ( 1,1 ) é:

y = 2 x - 1

x 2 = y + 1 2

E para a função y = k x 1 3 passar pelos pontos ( 1,1 ) o valor de k terá que ser:

1 = k × 1 1 3 → k = 1

Logo isolando x nessa equação temos:

x 1 = y 3

O comprimento dessa linha será:

L = x 2 - x 1 = y + 1 2 - y 3

Como a largura dessa linha vale d y logo o elemento de área desse gráfico valerá:

d A = y + 1 2 - y 3 d y

Com y variando de 0 até 1 .

O valor de x m será:

x m = x 2 + x 1 2 = y + 1 2 + y 3 2

E o valor de y m será o próprio y .

Passo 2

Calculando a área teremos:

A = ∫ 0 1 y + 1 2 - y 3 d y = y 2 4 + y 2 - y 4 4 0 1 = 1 4 + 1 2 - 1 4 = 1 2

Para achar a coordenada x do centroide precisamos fazer:

x - = ∫ x m d A A

Fazendo ∫ x m d A temos:

∫ x m d A = ∫ 0 1 1 2 y + 1 2 + y 3 y + 1 2 - y 3 d y

= 1 2 ∫ 0 1 1 4 y + 1 2 - y 6 d y

= 1 2 ∫ 0 1 1 4 y 2 + 2 y + 1 - y 6 d y = 1 2 1 4 y 3 3 + y 2 + 1 - y 7 7 0 1

= 1 2 1 4 1 3 + 1 + 1 - 1 7 = 37 168

Agora fazendo o calculo de x - :

x - = 37 168 1 2 = 37 84

Passo 3

Agora para encontrar a coordenada y do centroide temos que fazer:

y - = ∫ y m d A A

Fazendo ∫ y m d A temos:

∫ y m d A = ∫ 0 1   y ( y + 1 2 - y 3 d y = ∫ 0 1 y 2 + y 2 - y 4 d y

= y 3 6 + y 2 4 - y 5 5 0 1 = 1 6 + 1 4 - 1 5 = 13 60

Fazendo o cálculo de y - temos:

y - = 13 60 1 2 = 13 30

Resposta

x - = 37 84

y - = 13 60

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y - da área.
Determine a área e o centroide x - ,y - da área.
Determine a massa e a localização do centro de massa x - da barra se sua massa por unidade de comprimento é m = m 0 ( 1 + x / L ) .
Determine a área e o centroide ( x - , y - ) da área.
Determine a área e o centroide x - ,y - da área.