Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 77
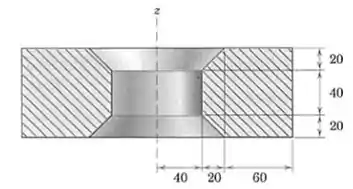
O corpo mostrado em seção transversal é a metade de um anel circular obtido pela revolução de 180 graus da área sombreada em torno do eixo . Determine a área superficial A do corpo.
Passo 1
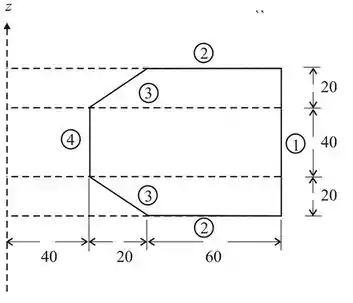
Vamos primeiro achar a área com base numa visão melhor da imagem abaixo, dividindo em 4 áreas e somando tudo no final!!
Passo 2
Considerando as faces finais:
Resposta
Exercícios de Livros Relacionados
Determine por integração direta os valores de x - para os dois sólidos obtidos passando-se um plano de corte vertical através da forma dada na Fig. 5.21. O plano de corte é paralelo à base da forma da
Sabendo que dois topos iguais foram removidos da esfera de madeira de diâmetro 250 mm, determine a área total da superfície da parte restante.
Determine por integração direta o centroide da área mostada na figura. Demonstre sua resposta em termos de a e h .
Determine o centroide do sólido obtido pela rotação da área sombreada da figura em torno do eixo x .
Determine por integração direta o centroide da área mostada na figura. Demonstre sua resposta em termos de a e b .