A área de um setor circular é girada de 180° em torno do eixo y. Determine o volume do corpo resultante, o qual é parte de uma esfera.
Passo 1
FALA AE MEU QUERIDO, simbora para mais uma? Essa questão é apenas sobre a aplicação do teorema de Pappus, MAS ANTES, vamos falar um pouquinho sobre o corpo (lindo e maravilhoso),
O CORPO É UM SETOR CIRCULAR, portanto, precisaremos medir o centro de massa de um setor circular juntamente com a sua área, de certo que já deves saber as equações que usaremos para isso, então...Não sabe? O QUE ESTÁ FAZENDO AQUI? Tá muito apressado, sai daqui e procura no Responde aí o conteúdo de centro de massa, enfim, orientados os perdidos, permita-me apresentá-lo as equações que usaremos:
É MUITA COISA, calma, vamos para a aplicação disso, SIGAM-ME OS BONS!
Passo 2
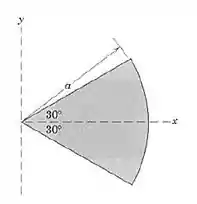
Analisando a figura, obtemos os valores do raio e do ângulo: r = a, = 30° = , com isso, podemos aplicar os dados coletados nas equações e desse modo, conseguir o resultado, então, SIMBORA:
COM ISSO, temos a distância do centro de massa ao eixo y, BORA CALCULAR A ÁREA:
YUPIE, com esses valores, agora podemos jogar tudo na equa��ão para descobrir o volume, lembrando que é o ângulo de revolução realizado no eixo y:
YEAAH, menos uma, é isso aí, BORA CONTINUAR NOS ESTUDOS, até a próxima.